高中物理焦耳定律试题

在如图所示的电路中，两平行正对金属板A、B水平放置，两板间的距离d=4.0cm。电源电动势E=400V，内电阻r=20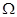，电阻R₁=1980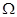。闭合开关S，待电路稳定后，将一带正电的小球（可视为质点）从B板上的小孔以初速度v₀=1.0m/s竖直向上射入两板间，小球恰好能到达A板。若小球所带电荷量q=1.0×10^-7C，质量m=2.0×10^-4kg，不考虑空气阻力，忽略射入小球对电路的影响，取g=10m/s²。求：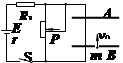

（1）A、B两金属板间的电压的大小U；
（2）滑动变阻器消耗的电功率P_滑。

某同学将一直流电源的总功率P_E、输出功率P_R和电源内部的发热功率P_r随电流I变化的图线画在了同一坐标系上，如图中的A.B.c所示，根据图线可知

A.反映P_r变化的图线是b
B.电源电动势为8 V
C.电源内阻为1Ω
D.当电流为0.5 A时，外电路的电阻为6Ω

如图所示，MN、PQ两条平行的光滑金属轨道与水平面成θ角固定，轨距为d。空间存在匀强磁场，磁场方向垂直于轨道平面向上，磁感应强度为B。P、M间接有阻值为3R的电阻。Q、N间接有阻值为6R的电阻，质量为m的金属杆ab水平放置在轨道上，其有效电阻为R。现从静止释放ab，当它沿轨道下滑距离s时，达到最大速度。若轨道足够长且电阻不计，重力加速度为g。求：

（1）金属杆ab运动的最大速度；
（2）金属杆ab运动的加速度为时，金属杆ab消耗的电功率；
（3）金属杆ab从静止到具有最大速度的过程中，克服安培力所做的功。

有一个直流电动机，把它接入0．2V电压的电路时，电动机不转，测得流过电动机的电流是0.4A，若把它接入2V电压的电路中，电动机正常工作，工作电流是1.0A。求：
（1）电动机正常工作时的热功率为多大？输出功率为多大？
（2）如在正常工作时，转子突然被卡住，此时电动机的发热功率多大？

不计电阻的光滑平行轨道EFG、PMN构成相互垂直的L型，磁感应强度为B的匀强磁场方向与水平的EFMP平面夹角θ（θ<45°）斜向上，金属棒ab、cd的质量均为m、长均为L、电阻均为R。ab、cd由细线通过角顶处的光滑定滑轮连接，细线质量不计，ab、cd与轨道正交，已知重力加速度为g。

（1）求金属棒的最大速度v_max；
（2）当金属棒速度为v时，且v小于最大速度v_max时，求机械能损失的功率P₁和电阻的发热功率P₂。

如图电路中，电池组的电动势E=42V，内阻r=2Ω，定值电阻R=20Ω，D是电动机，其线圈电阻R′=1Ω．电动机正常工作时，理想电压表示数为20V．求：

（1）通过电动机的电流是多少？
（2）电动机输出的机械功率为多少？

一辆以蓄电池为驱动能源的环保电动汽车，拥有三十多个座位，其电池每次充电仅需三至五个小时，蓄电量可让汽车一次性跑5.0×10⁵m，汽车时速最高可达1.8×10²km/h，汽车总质量为9.0×10³kg。驱动电机直接接在蓄电池的两极，且蓄电池的内阻为r=0.20Ω。当该汽车在某城市快速水平公交路面上以v＝90km/h的速度匀速行驶时，驱动电机的输入电流I＝1.5×10²A，电压U＝3.0×10²V，内电阻R_M=0.40Ω。在此行驶状态下（取g＝10 m/s²），求：
（1）驱动电机输入的电功率P_入；
（2）驱动电机的热功率P_热；
（3）驱动电机输出的机械功率P_机；
（4）蓄电池的电动势E。

如图所示电路中，电源电动势ε恒定，内阻r=1Ω，定值电阻R₃=5Ω。当电键S断开与闭合时，ab段电路消耗的电功率相等。则下列说法中正确的是 （电表均为理想表）

A．电阻R1、R2可能分别为4Ω、5Ω

B．电阻R1、R2可能分别为3Ω、6Ω

C．电键S断开时电压表的示数一定大于S闭合时的示数

D．电键S断开与闭合时电压表的示数变化量大小与电流表的示数变化量大小之比一定等于6Ω

如图所示的电路中，电源电动势E=9V，电阻R₁=2.5Ω，R₂=3Ω，滑动变阻器R的最大阻值是6Ω。当滑动变阻器R连入电路中的阻值调到3Ω时，理想电流表的示数为2A。求：

（1）电源的内阻。
（2）调节变阻器的阻值，电流表的示数发生变化但没有超过量程，求电流表示数的最大值和最小值。
（3）当滑动变阻器R连入电路中的阻值调到6Ω时，变阻器R的耗电功率是多大？

如图所示的电路中，电源电动势E =" 6.0V" ，内阻r =" 0.6Ω" ，电阻R₂ =" 0.5Ω" ，当开关S断开时，电流表的示数为1.5A，电压表的示数为3.0V ，试求：

电阻R₁和R₃的阻值
当S闭合后，求电压表的示数和R₂上消耗的电功率

某电子天平原理如图所示，形磁铁的两侧为极，中心为极，两级间的磁感应强度大小均为，磁极的宽度均为的重物放在秤盘上时，弹簧被压缩，秤盘和线圈一起向下运动（骨架与磁极不接触），随后外电路对线圈供电，秤盘和线圈恢复到未放重物时的位置并静止，由此时对应的供电电流可确定重物的质量.已知线圈的匝数为，线圈的电阻为，重力加速度为。问：

（1）线圈向下运动过程中，线圈中感应电流是从端还是端流出？

（2）供电电流是从端还是端流入？求重物质量与电流的关系.

（3）若线圈消耗的最大功率为，该电子天平能称量的最大质量是多少

半径分别为和的同心圆形导轨固定在同一水平面上，一长为，质量为且质量分布均匀的直导体棒置于圆导轨上面，的延长线通过圆导轨的中心，装置的俯视图如图所示；整个装置位于一匀强磁场中，磁感应强度的大小为，方向竖直向下；在内圆导轨的点和外圆导轨的点之间接有一阻值为R的电阻（图中未画出）。直导体棒在水平外力作用下以角速度绕逆时针匀速转动，在转动过程中始终与导轨保持良好接触。设导体棒与导轨之间的动摩擦因数为μ，导体棒和导轨的电阻均可忽略，重力加速度大小为，

求：（1）通过电阻的感应电流的方向和大小；

（2）外力的功率。

如图所示，在a、b两端有直流恒压电源，输出电压恒为U_ab，R₂=40Ω，右端连接间距d=0.04m、板长l=10cm的两水平放置的平行金属板，板间电场视为匀强电场。闭合开关，将质量为m=1.6×10^-6kg、带电量q=3.2×10^-8C的微粒以初速度v₀=0.5m/s沿两板中线水平射入板间。当滑动变阻器接入电路的阻值为15Ω时，微粒恰好沿中线匀速运动，通过电动机的电流为0.5A。已知电动机内阻R₁=2Ω，取g=10m/s²。试问：
（1）输出电压为U_ab是多大？
（2）在上述条件下，电动机的输出功率和电源的输出功率？
（3）为使微粒不打在金属板上，R₂两端的电压应满足什么条件？

是一个电热毯示意电路图．R₀是电热毯中的电阻丝，R是与电热毯与电阻丝串联的电阻．电热毯上标有“220V 100W”字样，S是控制电热毯处于加热状态或保温状态的开关．

（1）用学过的公式推理说明开关S断开时，电热毯是处于加热状态还是保温状态？
（2）若要求在保温时电流通过电阻丝R₀每分钟有60J的电能转化为内能，电阻R的阻值是多大？

描绘小电珠的伏安特性曲线的实验电路如图，小电珠的额定电压是3.8V。
（1）根据实验数据在坐标系中描点如右图。试在坐标系中画出该小灯泡的伏安曲线。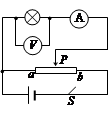

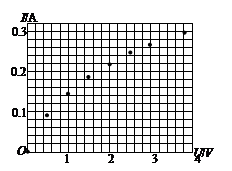
（2）根据图象，下列说法正确的是：
A.该小灯泡的额定功率为1.14W
B.小灯泡在1V电压下灯丝的电阻约为7.1Ω
C.小灯泡在2V电压下灯丝的电阻约为9.1Ω
D.小灯泡在不同电压下的电阻不相同是因为灯丝的电阻率随温度升高而减小
（3）关于该实验的系统误差，下列说法中正确的是
A.系统误差主要是由电压表的分流引起的
B.系统误差主要是由电流表的分压引起的
C.系统误差主要是由于忽略电源内阻引起的
D.系统误差主要是由读数时的估读引起的
（4）若将该灯泡接与r＝20Ω的电阻串联后接在U₀＝4V的电压两端，其实际功率是       W