在如图甲所示的电路中,电源电动势为3.0V,内阻不计,L1、L2、L3为3个相同规格的小灯泡,这种小灯泡的伏安特性曲线如图乙所示.当开关闭合后,下列关于电路中的灯泡的判断,正确的是( )
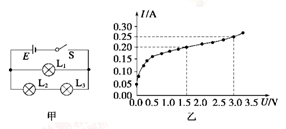
| A.灯泡L1的电阻为12Ω |
| B.通过灯泡L1的电流为灯泡L2的电流的2倍 |
| C.灯泡L1消耗的电功率为0.75 W |
| D.灯泡L2消耗的电功率为0.30 W |
如图所示,电路中a、b、c为三个相同的灯泡,每个灯泡的电阻大于电源内阻,当变阻器R的滑片P向上移动时,下列判断中正确的是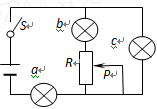
| A.a、b两灯变暗,c灯变亮 |
| B.a、b两灯变亮,c灯变暗 |
| C.电源输出功率增大 |
| D.电源内阻的热功率 |
如图所示,电动势为E,内阻不计的电源与三个灯泡和三个电阻相接,只闭合开关 ,三个灯泡都能正常工作,如果再合上
,三个灯泡都能正常工作,如果再合上 ,则下列表述正确的是
,则下列表述正确的是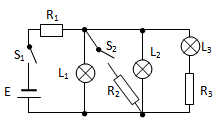
| A.电源的输出功率减小 | B.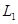 上消耗的功率减小 上消耗的功率减小 |
C.通过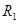 上的电流增大 上的电流增大 |
D.通过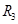 上的电流增大 上的电流增大 |
如图所示,导电物质为电子的霍尔元件位于两串联线圈之间,线圈中电流为I,线圈间产生匀强磁场,磁感应强度大小B与I成正比,方向垂直于霍尔元件的两侧面,此时通过霍尔元件的电流为IH,与其前后表面相连的电压表测出的霍尔电压UH满足:UH=k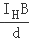 ,式中k为霍尔系数,d为霍尔元件两侧面间的距离.电阻R远大于RL,霍尔元件的电阻可以忽略,则( )
,式中k为霍尔系数,d为霍尔元件两侧面间的距离.电阻R远大于RL,霍尔元件的电阻可以忽略,则( )
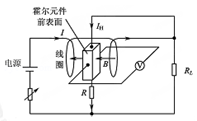
| A.霍尔元件前表面的电势低于后表面 |
| B.若电源的正负极对调,电压表将反偏 |
| C.IH与I成正比 |
| D.电压表的示数与RL消耗的电功率成正比 |
某同学将一直流电源的总功率PE、输出功率PR和电源内部的发热功率Pr随电流I变化的图线画在同一坐标系中,如右图中的a、b、c所示。则下列说法中正确的是( )
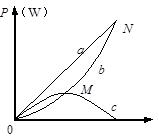
A.图线b表示输出功率PR随电流I变化的关系
B.在a、b、c三条图线上分别取横坐标相同的A、B、C 三点,这三点的纵坐标一定满足关系PA=PB+PC
C.图中a线最高点对应的功率为最大输出功率
D.b、c线的交点M与a、b线的交点N的横坐标之比为1:2,纵坐标之比为 1:4
一个直流电动机,线圈电阻恒定为0.5Ω;若把电动机接2.0V电压能正常工作,此时经过线圈的电流是1.0A,则电动机的输出功率P出是
| A.P出=2.5W | B.P出=2W | C.P出=1.5W | D.P出=1W |
在某段电路中,其两端电压为U,通过的电流为I,通电时间为t,若该电路电阻为R,则关于电功和电热的关系,下列结论不正确的是( )
| A.在任何电路中,电功W=UIt=I2Rt |
| B.在任何电路中,电功为UIt,电热为I2Rt |
| C.在纯电阻电路中,UIt=I2Rt |
| D.在非纯电阻电路中,UIt>I2Rt |
如图所示,两根平行的光滑金属导轨M、N,电阻不计,相距L="0.2" m,上边沿导轨垂直方向放一个质量为m=4×10-2 kg的金属棒ab,ab的电阻R0="0.5" Ω.,两金属导轨一端通过电阻R=2 Ω和电源相连.电源电动势E=6 V,内阻r=0.5 Ω,如果在装置所在的区域加一个水平向右的匀强磁场,使ab对导轨的压力恰好是零,并使ab处于静止.求:
(1)闭合电路中的电流是多大?
(2)磁感应强度B的大小
(3)导体棒ab产生的热功率P热 是多少瓦特?
在光控电路中,光敏电阻阻值随着光照强度的变化可实现对电路相关物理量的调节,如图所示,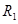 为定值电阻,
为定值电阻,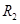 为半导体光敏电阻,C为电容器,当
为半导体光敏电阻,C为电容器,当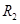 上光照强度减弱时
上光照强度减弱时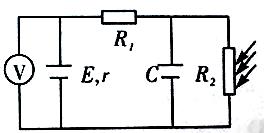
| A.电压表的读数减小 |
| B.电容器C的带电量增大 |
| C.电容器C两极板间的电场强度减小 |
D.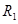 消耗的电功率增大 消耗的电功率增大 |
如图所示,两根光滑的金属导轨,平行放置在倾角为θ的斜面上,导轨的左端接有电阻R,导轨自身的电阻不计,磁场方向垂直于斜面向上,质量为m、电阻不计的金属棒ab在沿着斜面、与棒垂直的恒力F作用下沿导轨匀速上滑h高度,在此过程中( )

| A.作用于金属棒上的各个力的合力所做的功等于零 |
| B.作用于金属棒上的各个力的合力所做的功等于mgh与电阻R上发出的焦耳热之和 |
| C.恒力F与安培力的合力所的功等于零 |
| D.恒力F与安培力的合力所做的功等于电阻R上发出的焦耳热 |
关于电功和电热的计算,下列说法正确的是( )
| A.如果是纯电阻电路,电热可用公式W = I2Rt计算,但不能用公式W = UIt计算 |
| B.如果是纯电阻电路,电功可用公式W = UIt计算,也可用公式W = I2Rt计算 |
| C.如果不是纯电阻电路,电功只能用公式W = I2Rt计算 |
| D.如果不是纯电阻电路,电热可用公式W = I2Rt计算,也可用公式W = UIt计算 |
一白炽灯泡的额定功率与额定电压分别为36 W与36 V。若把此灯泡接到输出电压为18 V的电源两端,则灯泡消耗的电功率( )
| A.等于36 W | B.小于36 W,大于9 W |
| C.等于9 W | D.小于9 W |
在雨雪冰冻天,为清除高压输电线上的凌冰,有人设计了这样的融冰思路:利用电流的热效应除冰.若在正常供电时,高压线上送电电压为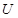 ,电流为
,电流为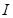 ,热损耗功率为
,热损耗功率为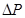 ;除冰时,输电线上的热耗功率需变为
;除冰时,输电线上的热耗功率需变为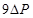 ,则除冰时(认为输电功率和输电线电阻不变)输电电流为 , 输电电压为 .
,则除冰时(认为输电功率和输电线电阻不变)输电电流为 , 输电电压为 .