两个完全相同的小金属球(皆可视为点电荷),所带电荷量之比为5∶1,它们在相距一定距离时相互作用的吸引力为F1,如果让它们充分接触后再放回各自原来的位置上,此时相互作用力变为F2,则F1∶F2为( )
| A.5∶2 | B.5∶4 | C.5∶6 | D.5∶9 |
A、B两个带同种电荷的绝缘金属小球,半径为r,球心相距3r,A带电荷量Q1,B带电荷量Q2,则A、B间相互作用力 ( )
A.无法确定 B.等于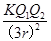
C.大于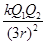 D.小于
D.小于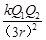
在光滑绝缘的水平面上,有两个相距较近的带同种电荷的小球,将它们由静止释放,则两球间( )
| A.距离变大,库仑力变大 | B.距离变大,库仑力变小 |
| C.距离变小,库仑力变大 | D.距离变小,库仑力变小 |
有两个点电荷,所带电荷量分别为 和
和 ,相距为r,相互作用力为F,为了使它们之间的作用力增大为原来的2倍,下列做法可行的是
,相距为r,相互作用力为F,为了使它们之间的作用力增大为原来的2倍,下列做法可行的是
A.仅使 增大为原来的2倍 增大为原来的2倍 |
B.仅使 减小为原来的一半 减小为原来的一半 |
C.使 和 和 都增大为原来的2倍 都增大为原来的2倍 |
| D.仅使r减小为原来的一半 |
真空中有两个固定的带正电的点电荷,其电量Q1>Q2,点电荷q置于Q1、Q2连线上某点时,正好处于平衡,则
| A.q一定是正电荷 | B.q一定是负电荷 | C.q离Q2比离Q1远 | D.q离Q2比离Q1近 |
已知如图,带电小球A、B的电荷分别为QA、QB,OA=OB,都用长L的丝线悬挂在O点。静止时A、B相距为d。为使平衡时AB间距离减为d/2,可采用以下哪些方法( )
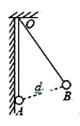
A.将小球A、B的质量都增加到原来的2倍
B.将小球B的质量增加到原来的8倍
C.将小球A、B的电荷量都减小到原来的一半
D.将小球A、B的电荷量都减小到原来的一半,同时将小球B的质量增加到原来的2倍
下列说法正确的是
| A.库仑定律适用于点电荷,点电荷其实就是体积很小的球体 |
B.根据F=k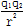 ,当两电荷的距离趋近于零时,静电力将趋向无穷大 ,当两电荷的距离趋近于零时,静电力将趋向无穷大 |
| C.若点电荷q1的电荷量大于q2的电荷量,则q1对q2的静电力大于q2对q1的静电力 |
| D.所有带电体的电荷量一定等于元电荷的整数倍 |
下列有关物理方法和创新实验的叙述正确的是
| A.库仑发明了扭秤,巧妙而准确地测量出了电荷间的静电力 |
| B.奥斯特发现了电流的磁效应 |
| C.安培开创了科学实验之先河,测出了万有引力常数 |
| D.法拉第发现了电磁感应现象,并制作了世界上第一台发电机 |
用两根等长的细线各悬一个小球,并挂于同一点,已知两球质量相等,当它们带上同种电荷时,相距L而平衡,如图所示.若使它们的带电量都减少一半,待它们重新平衡后,两球间距离
| A.大于L/2 | B.等于L/2 | C.小于L/2 | D.等于L |
真空中有两个静止的点电荷,它们之间的相互作用力F,若它们的带电量都增大为原来的2倍,它们之间的相互作用力变为( )
| A.F/2 | B.F | C.4F | D.16F |
真空中有两个点电荷,它们之间的静电力为F,若把两个点电荷的电量都增加到原来的2倍,距离也增加到原来的2倍,则它们之间的库仑力将变为
| A.F | B.2F | C.4F | D.8F |
如图所示,两个等量异号的点电荷在其连线的中垂线上有与连线中点O等距离的两点a、b,在连线上有距中点O等距离的两点c、d,则下列场强大小关系式正确的是( )
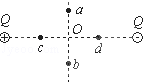
| A.Ea=Eb<Ec | B.Ea=EO=Eb | C.Ea<Ed | D.Ec>EO>Ed |
如图,一带有绝缘座的空心球壳A带有4×10-8C的正电荷,一带绝缘柄的金属球B带有-2×10-8C的负电荷,通过A上的小孔使B和A的内表面接触,则A、B各自带电为: ( )

A.QA=10-8C,QB =10-8C
B.QA =0,QB =2×10-8C
C.QA=2×10-8C,QB =0
D.QA =-2×10-8C,QB =2×10-8C;