高中物理库仑定律选择题

已知如图，带电小球A、B的电荷分别为Q_A、Q_B，OA=OB，都用长L的丝线悬挂在O点．静止时A、B相距为d．为使平衡时AB间距离减为，可采用以下哪些方法(     )

A．将小球A、B的质量都增加到原来的2倍
B．将小球B的质量增加到原来的8倍
C．将小球A、B的电荷量都减小到原来的一半
D．将小球A、B的电荷量都减小到原来的一半，同时将小球B的质量增加到原来的2倍

如图，A.b两个带电小球，质量分别为，用绝缘细线悬挂，细线无弹性且不会被拉断．两球静止时，它们距水平地面的高度均为h（h尽够大），绳与竖直方向的夹角分别为和.若剪断细线Oc，空气阻力不计，两球电量不变，重力加速度为g．则下列说法正确的是

A．a球先落地，b球后落地
B．落地时，A.b两球的动能和为（m_a＋m_b）gh
C．整个运动过程中，A.b系统的机械能守恒
D．落地时，A.b水平速度不为零并且有大小相等，且方向相反

真空中有两个电量之比为1:7的静止的点电荷，它们之间的库仑引力为 F，两者相互接触后再放回原来的位置上，则相互作用力为

A．3F/7

B．4 F /7

C．9 F /7

D．16 F /7

如图所示，竖直绝缘墙壁上的Q处有一固定的质点A，在Q正上方的P点用绝缘丝线悬挂另一质点B，A、B两质点因为带电而相互排斥，使悬线与竖直方向成θ角，现通过某种方法使A、B的带电荷量均变为原来的两倍，则悬线对悬点P的拉力大小将（ ）

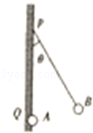
A．变为原来的      B．保持不变
C．变为原来的2倍    D．变为原来的4倍

在真空中有两个固定的点电荷，它们之间的静电力大小为F。现保持它们之间的距离不变，而使它们的电荷量都变为原来的2倍，则它们之间的静电力大小为(    )

A．F

B．F

C．2F

D．4F

关于物理学家和他们的贡献，下列说法中正确的是

A．奥斯特发现了电流的磁效应

B．库仑提出了库仑定律，并最早用实验测得元电荷e的数值

C．开普勒发现了行星运动的规律，并通过实验测出了万有引力常量

D．牛顿不仅发现了万有引力定律，而且提出了场的概念

如图所示，水平天花板下用长度相同的绝缘细线悬挂起来的两个相同的带电小球A、B，左边放一个带正电的固定球+Q时，两悬线都保持竖直方向，小球A与固定球+Q的距离等于小球A与小球B的距离。下列说法中正确的是（  ）

A．A球带正电，B球带负电，并且A球带电荷量较大
B．A球带负电，B球带正电，并且A球带电荷量较小
C．A球带负电，B球带正电，并且A球带电荷量较大
D．A球带正电，B球带负电，并且A球带电荷量较小

两个点电荷相距为L带电量均为q它们之间的静电力为F，现把距离增大为2L，电量均增为2q
则静电力变为   (   ）

A．2F

B．F

C．F/2

D．F/4

真空中有两个静止的点电荷，它们之间静电力的大小为F．如果保持这两个点电荷之间的距离不变，而将它们的电荷量都变为原来的4倍，那么它们之间静电力的大小变为

A．

B．

C．

D．

真空中有两个静止的点电荷，它们之间静电力的大小为F．如果保持这两个点电荷之间的距离不变，而将它们的电荷量都变为原来的4倍，那么它们之间静电力的大小变为（  ）

A．

B．

C．4F

D．16F

A、B、C三点在同一直线上，AB∶BC＝1∶2，B点位于A、C之间，在B处固定一电荷量为Q的点电荷。当在A处放一电荷量为＋q的点电荷时，它所受到的电场力为F；移去A处电荷，在C处放电荷量为－2q的点电荷，其所受电场力为(     )
A．－F/2        B．F/2        C．－F         D．F

下列描述中符合物理学史实的是

A．奥斯特提出了分子电流假说，并很好地解释了一些磁现象

B．安培提出了用电场线来描述电场的观点

C．库仑发现了真空中两个静止电荷之间的相互作用规律

D．法拉第根据小磁针在通电导线周围的偏转发现了电流的磁效应

下列说法正确的是（ ）

A．元电荷就是质子

B．带电体所带电荷量一定是元电荷的整数倍

C．点电荷一定是带电量很少的带电体

D．处于静电平衡的导体的内部可能有净电荷

对于场强，本节出现了E =和E =k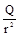两个公式，你认为下列认识正确的是（   ）

A．q表示场中的试探电荷、Q表示场源电荷

B．第一个公式适用于包括点电荷在内的所有场源的电场求场强，且E的方向和F一致

C．E随q的增大而减小，随Q的增大而增大

D．从第二个公式看，拿走Q后，E就不存在了

导体A带5Q的正电荷，另一完全相同的导体B带Q的负电荷，将两导体接触一会儿后再分开，则B导体的带电荷量为(  )

A．－Q

B．Q

C．2Q

D．4Q