如图所示,两个带有同种电荷的小球,用绝缘细线悬挂于O点,若q1>q2,l1>l2,平衡时两球到过O点的竖直线的距离相等,则( )
| A.m1>m2 |
| B.m1=m2 |
| C.m1<m2 |
| D.无法确定 |
两个完全相同的金属小球A、B,球A所带电荷量为+4Q,球B不带电.现将球B与球A接触后,移到与球A相距为d处(d远远大于小球半径).已知静电力常量为k,则此时两球A、B之间相互作用的库仑力大小是( )
A.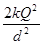 B.
B.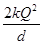 C.
C.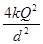 D.
D.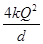 .
.
如图所示,三个点电荷ql,q2,q3固定在一条直线上,q2与q3 的距离为ql与q2的距离的2倍,每个电荷所受静电力的合力均为零。由此可以判定,三个电荷的电量之比ql:q2:q3为( )
| A.-9:4:-36 | B.9:4:36 | C.-3:2:-6 | D.3:2:6 |
把系在丝线上的带电小球先后挂在横杆上的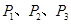 位置,可以比较小球在三个不同位置受到静电力的大小。这个力的大小可以通过丝线偏离竖直方向的角度显示出来。该实验采用的方法是________(填选项前的字母)
位置,可以比较小球在三个不同位置受到静电力的大小。这个力的大小可以通过丝线偏离竖直方向的角度显示出来。该实验采用的方法是________(填选项前的字母)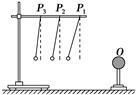
| A.微小量放大法 | B.等效替代法 | C.控制变量法 | D.理想模型法 |
半径为R的大球O被内切地挖去半径为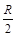 的小球
的小球 ,余下的部分均匀地带有电荷量Q。今在两球球心连线
,余下的部分均匀地带有电荷量Q。今在两球球心连线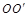 的延长线上,距大球球心O的距离为r(r>R)处放置一个点电荷q,求q所受的力。你可以不必进行复杂的计算,而是根据所学的物理知识和物理方法进行分析,从而判断解的合理性。
的延长线上,距大球球心O的距离为r(r>R)处放置一个点电荷q,求q所受的力。你可以不必进行复杂的计算,而是根据所学的物理知识和物理方法进行分析,从而判断解的合理性。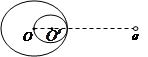
A.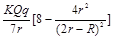 |
B.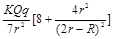 |
C.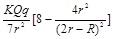 |
D.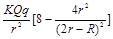 |
在一绝缘支架上,固定着一个带正电的小球A,A又通过一长为10cm的绝缘细绳连着另一个带负电的小球B,B的质量为0.1kg,电荷量为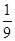 ×10-6C,如图所示,将小球B缓缓拉离竖直位置,当绳与竖直方向的夹角为60°时,将其由静止释放,小球B将在竖直面内做圆周运动.已知释放瞬间绳刚好张紧,但无张力. g取10m/s2.求
×10-6C,如图所示,将小球B缓缓拉离竖直位置,当绳与竖直方向的夹角为60°时,将其由静止释放,小球B将在竖直面内做圆周运动.已知释放瞬间绳刚好张紧,但无张力. g取10m/s2.求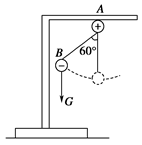
(1)小球A的带电荷量;
(2)释放瞬间小球B的加速度大小;
(3)小球B运动到最低点时绳的拉力.
带等量异种电荷的点电荷固定在空间的A.B两点,CD为AB的中垂线,O为垂足,一个α粒子在由AB.CD确定的平面内运动.如图的四条弧形虚线中,哪些是α粒子的可能轨迹( )
A.①③ B.②④ C.③ D.①
如图,三个固定的带电小球a、b和c,相互间的距离分别为 , , 。小球c所受库仑力的合力的方向平行于a、b的连线。设小球a、b所带电荷量的比值的绝对值为K,则( )。
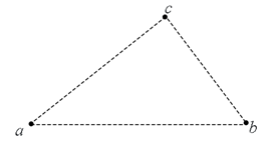
| A. |
a、b的电荷同号, |
B. |
a、b的电荷异号, |
| C. |
a、b的电荷同号, |
D. |
a、b的电荷异号, |
如图,空间存在一方向水平向右的匀强磁场,两个带电小球
和
用相同的绝缘细绳悬挂在水平天花板下,两细绳都恰好与天花板垂直,则( )

A. 和 都带正电荷
B. 和 都带负电荷
C. 带正电荷, 带负电荷
D. 带负电荷, 带正电荷
如图所示,一平行板电容器的电容为C,两板间的距离为d,上极板带正电,电荷量为Q,下极板带负电,电荷量也为Q,它们产生的电场在很远处的电势为零。两个带异号电荷的小球用一绝缘刚性杆相连,小球所带的电荷量都为q,杆长为l,且l<d。现将它们从很远处移到电容器内板之间,处于图示的静止状态(杆与板面垂直),在此过程中静电力对两个小球所做总功的大小为(设两球移动过程中极板上电荷分布情况不变)( )

A. |
B.0 | C. |
D. |
如图所示,一电子沿等量异种点电荷的中垂直线由A→O→B匀速飞过,电子重力不计,则电子所受电场力的大小和方向变化情况是( )
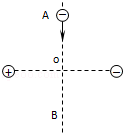
| A.先变大后变小,方向水平向左 |
| B.先变大后变小,方向水平向右 |
| C.先变小后变大,方向水平向左 |
| D.先变小后变大,方向水平向右 |
真空中两个完全相同、带异种电荷的导体小球A和B(视为点电荷),A带电荷量为+4Q,B带电荷量为-2Q,彼此间的引力为F.把两导体小球互相接触后再移回原来各自的位置,这时A 和B之间的作用力为F′,则F与F′之比为( )
| A.8:3 | B.8:1 | C.1:8 | D.4:1 |
如图所示,一电荷量为+Q的点电荷甲固定在光滑绝缘的水平面上的O点,另一电荷量为+q、质量为m的点电荷乙从A点经C以v0="2" m/s的初速度沿它们的连线向甲运动,到达B点时的速度为零,已知AC=CB,φA="3" V,φB="5" V,静电力常量为k,则( )
| A.φC>4V |
| B.φC="4" V |
| C.点电荷乙的比荷为1 C/kg |
| D.点电荷乙的比荷为2 C/kg |
如图所示,光滑平面上固定金属小球A,用长L0的绝缘弹簧将A与另一个金属小球B连接,让它们带上等量同种电荷,弹簧伸长量为x1;若两小球电量各漏掉一半,弹簧伸长量变为x2,则有( )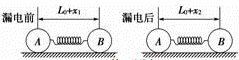
A. |
B. |
C. |
D.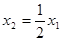 |