高中物理库仑定律试题

下列说法中正确的是 （  ）
A．由公式可知，电场中某点的场强与放在该点的检验电荷所受的电场力的大小成正比，与检验电荷的电量成反比
B．由公式可知，电场中A、B两点间电势差U_AB与在这两点之间移动电荷时电场力所做的功W_AB成正比，与电荷的电量q成反比
C．在库仑定律的表达式中， 是点电荷产生的电场在点电荷处的场强大小；而是点电荷产生的电场在点电荷处的场强大小
D．公式中的d为匀强电场中电势差为U的两点间的距离

下列说法正确的是(  )

A．根据电场强度定义式可知，与成正比，与成反比

B．电荷在电场中的受力方向就是该点电场强度方向

C．库仑定律适用于真空中两个静止点电荷间的相互作用

D．从公式可知，在以点电荷为圆心的圆周上，场强处处相同

两个分别带有电荷量为－Q和＋3Q的相同金属小球（均可视为点电荷），固定在相距为r的两处，它们间库仑力的大小为F.两小球相互接触后将其固定距离变为，则两球间库仑力的大小为（ ）．

A．

B．

C．

D．12

真空中有两个静止点电荷，它们之间的静电引力为F．如果它们之间的距离增大为原来的2倍，而其中一个点电荷的电荷量减少为原来的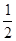，则它们之间的作用力的大小变为(     )

A．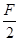

B．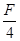

C．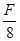

D．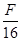

如图所示，A、B是系在绝缘细线两端，带有等量同种电荷的小球（可视为质点），同种电荷间的排斥力沿两球心连线向相反方向，其中m_A=0.3kg，现将绝缘细线通过O点的光滑定滑轮，将两球悬挂起来，两球平衡时，OA的线长等于OB的线长，A球紧靠在光滑绝缘竖直墙上，B球悬线OB偏离竖直方向60⁰角，g＝10 m/s²，求：


（1）B球的质量；   （2）细绳中的拉力大小

下列说法正确的是(     )

A．库仑在研究电荷间相互作用时，提出了“电场”的概念

B．电源的电动势跟电源内非静电力做的功成正比，跟通过电源的电荷量成反比

C．将正点电荷从场强为零的一点移动到场强为零的另一点，电场力做功不一定为零

D．通电导线在某点不受磁场力的作用，则该点的磁感应强度一定为零

真空中有两个静止的点电荷，它们之间的作用力为F，若它们的带电量都增大为原来的3倍，距离减少为原来的1/3，它们之间的相互作用力变为

A．F/3

B．F

C．9F

D．81F

两个相同的金属小球，所带电荷大小之比为1:7，相距为r，两者相互接触后再放回原来的位置上，则它们之间的库仑力可能为原来的（   ）

A．4：7

B．3：7

C．16：7

D．9：7

真空中两个点电荷，它们之间的静电力为F，如果将两个点电荷的距离增大为原来的2倍，电量都增大为原来的2倍。它们之间静电力的大小为 （   ）

A．F/2

B．F

C．2F

D．4F

两个分别带有电荷量和+的相同金属小球（均可视为点电荷），固定在相距为的两处，它们之间的库仑力大小为。两小球相互接触后分开并将其固定距离变为，则现在两球间库仑力的大小为

A．

B．

C．

D．

两个完全相同的金属小球A、B，球A所带电荷量为＋5Q，球B所带电荷量为-Q．现将球B与球A接触后，移到与球A相距为d处（d远远大于小球半径）．已知静电力常量为k，则此时两球A、B之间相互作用的库仑力大小是（   ）
A．        B．        C．        D．.

如图所示，一电子沿等量异种电荷的中垂线由A→O→B匀速飞过，电子重力不计，则电子除受电场力外，所受的另一个力的大小和方向变化情况是

A．先变大后变小，方向水平向左	B．先变大后变小，方向水平向右
C．先变小后变大，方向水平向左	D．先变小后变大，方向水平向右

两个带正电的小球，放在光滑的水平绝缘板上，它们相距一定距离．若同时释放两球，它们的加速度之比将

A．保持不变

B．先增大后减小

C．增大

D．减小

P是点电荷Q电场中的一点，P到点电荷Q的距离r=0.1m。将一个电荷量的点电荷放到P点，受到的电场力，已知静电力常量。求：
（1）点电荷Q在P处的电场强度的大小
（2）点电荷Q的电荷量

两个等量异种的点电荷十Q和一Q，相距为r，在它们连线的中点O处放置另一点电荷q，如图所示，则q所受的电场力的大小等于：（  ）

A．4kQq/ r^2；	B．8kQq/r^2；
C．kQq/ r^2；	D．2kQq/ r^2。