如图所示,Q1、Q2为两个固定点电荷,其中Q1带正电,它们连线的延长线上有a、b两点.一正试探电荷以一定的初速度沿直线从b点开始经a点向远处运动,其速度图象如图所示.则 ( )
| A.Q2带正电 |
| B.Q2带负电 |
| C.该试探电荷从b到a的过程中电势能增大 |
| D.该试探电荷从b到a的过程中电势能减小 |
A、D两点各放有电量为十Q和十3Q的点电荷,A、B、C、D四点在同一直线上,且AB=BC=CD。现将一正电荷从B点沿直线移到C点,则( )
A.电势能一直减小
B.电势能一直增加
C.电势能先减小后增加
D.电势能先增加后减小
如图4所示,将一个半径为r的不带电的金属球放在绝缘支架上,金属球的右侧放置一个电荷量为Q的带正电的点电荷,点电荷到金属球表面的最近距离也为r。由于静电感应在金属球上产生感应电荷。设静电力常量为k。则关于金属球内的电场以及感应电荷的分布情况,以下说法中正确的是 ( )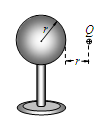
| A.电荷Q与感应电荷在金属球内任意位置激发的电场场强都是等大且反向的 |
B.感应电荷在金属球球心处激发的电场场强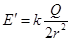 ,方向向右 ,方向向右 |
| C.感应电荷全部分布在金属球的表面上 |
| D.金属球右侧表面的电势高于左侧表面 |
如图所示,A、B是两个带有绝缘支架的金属球,它们原来均不带电,并彼此接触。现使带负电的橡胶棒C靠近A(C与A不接触),然后先将A、B分开,再将C移走。关于A、B的带电情况,下列判断正确的是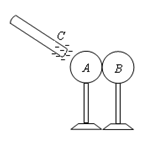
A.A带正电,B带负电
B.A带负电,B带正电
C.A、B均不带电
D.A、B均带正电
关于物理学史的下列说法中不正确的是: ( )
| A.法拉第通过实验研究确认真空中两点电荷之间相互作用力的规律 |
| B.元电荷e的数值最早由密立根测得 |
| C.法拉第第一个采用电场线描述电场 |
| D.夜间高压线周围出现的绿色光晕,其实是一种微弱的尖端放电现象 |
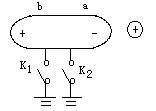
如图所示,把一个不带电的枕型导体靠近带正电的小球,由于静电感应,在a,b端分别出现负、正电荷,则以下说法正确的是:
( )
| A.闭合K1,有电子从枕型导体流向大地 |
| B.闭合K2,有电子从枕型导体流向大地 |
| C.闭合K1,有电子从大地流向枕型导体 |
| D.闭合K2,没有电子通过K2 |
关于点电荷的说法,下列正确的是
A.体积很大的带电体不 能看成点电荷 能看成点电荷 |
| B.物体带电量很小时,可以看作点电荷 |
| C.点电荷是理想化的物理模型 |
| D.点电荷的带电量一定是1.6×10-19 C |
如图1-1-7所示,左边是一个原先不带电的导体,右边C是后来靠近的带正电的导体球,若用绝缘工具沿图示某条虚线将导体切开,分导体为A、B两部分,这两部分所带电荷量的数值分别为QA、QB,则下列结论正确的是( )
| A.沿虚线d切开,A带负电,B带正电,且QA>QB |
| B.只有沿虚线b切开,才有A带正电,B带负电,且QA=QB |
| C.沿虚线a切开,A带正电,B带负电,且QA<QB |
| D.沿任意一条虚线切开,都有A带正电,B带负电,而QA、QB的值与所切的位置有关 |
挂在绝缘细线下的两个轻质小球,表面镀有金属薄膜,由于电荷的相互作用而靠近或远离,分别如图1-1-4甲、乙所示,则( )
| A.甲图中两球一定带异种电荷 |
| B.乙图中两球一定带同种电荷 |
| C.甲图中至少有一个带电 |
| D.乙图中两球至多有一个带电 |

甲物体与乙物体相互摩擦,没有其他物体参与电荷的交换,发现甲物体带了9.6×10-16 C的正电荷.以下结论正确的是( )
| A.甲物体失去了6×103个电子 | B.乙物体失去了6×103个电子 |
| C.乙物体带9.6×10-16 C的负电荷 | D.乙物体带9.6×10-16 C的正电荷 |
如图所示,三个质量相等的粒子,其中一个带正电荷,一个带负电荷,一个不带电荷,以相同初速度v0沿中央轴线进入水平放置的平行金属板间,最后分别打在正极板上的A、B、C处.则( )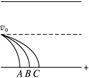
A.打在极板A处的粒子带负电荷,打在极板B处的粒子不带电,打在极板C处的粒子带正电荷
B.三个粒子在电场中的运动时间相等
C.三个粒子在电场中运动时的加速度aA>aB>aC
D.三个粒子打到极板上时的动能EkA<EkB<EkC
a、b是两个点电荷,它们的电荷量分别为Q1、Q2,MN是ab连线的中垂线,P是中垂线上的一点.下列情况中能使P点场强方向指向MN的左侧的是( )
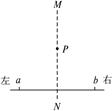
| A.Q1、Q2都是正电荷,且Q1<Q2 |
| B.Q1是正电荷,Q2是负电荷,且Q1>|Q2| |
| C.Q1是负电荷,Q2是正电荷,且|Q1|<Q2 |
| D.Q1、Q2都是负电荷,且|Q1|>|Q2| |
如图所示,电荷量为Q1、Q2的两个正点电荷分别置于A点和B点,两点相距L.在以L为直径的光滑绝缘半圆环上,穿着一个带电荷量为+q的小球(视为点电荷),在P点平衡.不计小球的重力,那么,PA与AB的夹角α与Q1、Q2的关系应满足( )

A.tan3α= |
B.tan2α= |
C.tan3α= |
D.tan2α= |