高中物理封闭气体压强试题

一定质量的理想气体在某一过程中，外界对气体做功7.0×10⁴ J，气体内能减少1.3×10⁵ J，此过程中
（1）气体从外界吸热还是对外放热？
(2）求吸收或者放出的热量为多少？

如图所示，在弹簧秤下，吊一粗细均匀、一端开口的直玻璃管，已知管的质量为m，横截面积为S，大气压强为p₀，管内上方为真空，管壁厚度不计且管口不与水银槽接触，则弹簧秤示数为(     )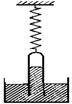

A．mg+p0S	B．mg
C．p0S	D．mg-p0S

气体内能是所有气体分子热运动动能和势能的总和，其大小与气体的状态有关，分子热运动的平均动能与分子间势能分别取决于气体的     （     ）

A．温度和体积

B．体积和压强

C．温度和压强

D．压强和温度

对一定量的气体，下列说法正确的是：（  　）

A．气体分子的热运动越剧烈，气体的温度就越高

B．气体体积是指所有气体分子的体积之和

C．气体对器壁的压强是由大量气体分子对器壁频繁碰撞而产生的

D．当气体膨胀时，气体的分子势能减小，因而气体的内能一定减少

关于密闭容器中气体的压强，下列说法中正确的是(     )

A．是由于气体分子相互作用产生的	B．是由于气体分子碰撞容器壁产生的
C．是由于气体的重力产生的	D．气体温度越高，压强就一定越大

一定质量的密闭气体，在温度升高的过程中，保持压强恒定，则在这个过程中

A．气体对外做功，内能减少

B．气体放出热量，内能增加

C．气体对外做功，吸收热量，内能不变

D．气体分子平均动能增加，分子间作用力减小

(8分)空气压缩机在一次压缩过程中，活塞对汽缸中的气体做功为2.0×10⁵ J，同
时气体的内能增加了1.5×10⁵ J．试问：
(1)此压缩过程中，气体________(选填“吸收”或“放出”)的热量等于________ J.
(2)若一定质量的理想气体分别按如图7所示的三种不同过程变化，其中表示等压变化的是________(选填“A”、“B”或“C”)，该过程中气体的内能________(选填“增加”、“减少”或“不变”)．

一定质量的非理想气体(分子间的作用力不可忽略)，从外界吸收了4.2×10⁵J的热量，同时气体对外做了6×10⁵J的功，则气体的内能改变了多少？气体的分子平均动能是增加还是减少？

上端开口的圆柱形气缸竖直放置，截面积为0.2ｍ^２的轻活塞将一定质量的气体和一形状不规则的固体Ａ封闭在气缸内．温度为300Ｋ时，活塞离气缸底部的高度为0.6ｍ；当在活塞加一质量为M的物体，再将气体加热到363Ｋ时，活塞上升了0.05ｍ此时气体的压强为1.1×10⁵pa，不计摩擦力及固体体积的变化，求物体Ａ的体积和M的大小．设大气压强为10⁵pa.

如图所示，气缸内装有一定质量的气体，气缸的截面积为S，其活塞为梯形，它的一个面与气缸成θ角，活塞与器壁间的摩擦忽略不计，现用一水平力F缓慢推活塞，汽缸不动，此时大气压强为P₀，则气缸内气体的压强P为：（  　）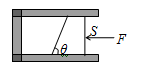

A．P=P0+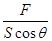	B．P=P0+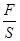
C．P=P0+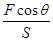	D．P=P0+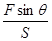

下列现象中与毛细现象有关的是 （      ）

A．砖块吸水

B．毛巾的一只角浸入水中，水会沿毛巾上升，使毛巾湿润

C．洗净的衣服在太阳下被晒干

D．自来水笔从墨水瓶里把墨水吸进笔中

一定质量的理想气体

A．先等压膨胀，再等容降温，其温度必低于起始温度

B．先等温膨胀，再等压压缩，其体积必小于起始体积

C．先等容升温，再等压压缩，其温度有可能等于起始温度

D．先等容升温，再等压压缩，其温度必低于起始温度

下列说法正确的是

A．一定质量的气体，在体积不变时，分子每秒与器壁平均碰撞次数随着温度降低而减小

B．晶体熔化时吸收热量，分子平均动能一定增大

C．空调既能制热又能制冷，说明在不自发地条件下热传递方向性可以逆向

D．外界对气体做功时，其内能一定会增大

E．生产半导体器件时，需要在纯净的半导体材料中掺人其他元素，可以在高温条件下利用分子的扩散来完成

物态变化现象在一年四季中随处可见，下列关于这些现象的说法中正确的是（  ）

A．春天的早晨经常出现大雾，这是汽化现象，要放出热量

B．夏天用干冰给运输中的食品降温，这是利用干冰熔化吸热

C．秋天的早晨花草上出现的小露珠，这是液化现象，要吸收热量

D．冬天在窗户玻璃上出现冰花，这是凝华现象，要放出热量

某压力锅结构如图所示。盖好密封锅盖，将压力阀套在出气孔上，给压力锅加热，当锅内气体压强达到一定值时，气体就把压力阀顶起。假定在压力阀被顶起时，停止加热。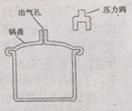

（1）若此时锅内气体的体积为V，摩尔体积为V₀，阿伏加德罗常数为N_A，写出锅内气体分子数的估算表达式。
（2）假定在一次放气过程中，锅内气体对压力阀及外界做功1J,并向外界释放了2J的热量。锅内原有气体的内能如何变化？变化了多少？
（3）已知大气压强P随海拔高度H的变化满足P=P₀（1-αH），其中常数α＞0。结合气体定律定性分析在不同的海拔高度使用压力锅，当压力阀被顶起时锅内气体的温度有何不同。