高中物理理想气体的状态方程计算题

(10分)、“拔火罐”是一种中医疗法，为了探究“火罐”的“吸力”，某人设计了如下图实验。圆柱状气缸（横截面积为S）被固定在铁架台上，轻质活塞通过细线与重物m相连，将一团燃烧的轻质酒精棉球从缸底的开关K处扔到气缸内，酒精棉球熄灭时（设此时缸内温度为t°C）密闭开关K，此时活塞下的细线刚好拉直且拉力为零，而这时活塞距缸底为L.由于气缸传热良好，重物被吸起，最后重物稳定在距地面L/10处。已知环境温度为27°C不变，mg/s与1/6大气压强相当，气缸内的气体可看做理想气体，
求t值。

如图所示，一根一端封闭的玻璃管，当l=0.96m，内有一段长h₁=0.20m的水银柱。当温度为t₁=27℃，开口端竖直向上时，封闭空气柱h₂=0.60m。问温度至少升到多高时，水银柱才能从管中全部溢出？（外界大气压相当于l₀=0.76m高的水银柱产生的压强）

圆柱形气缸筒长2l，截面积为S，缸内有活塞，活塞可以沿缸壁无摩擦不漏气的滑动，气缸置于水平面上，缸筒内有压强为p₀，温度为T₀的理想气体，气体体积恰好占缸筒容积的一半，如图所示。此时大气压也是p₀，弹簧的劲度系数为k，气缸与地面的最大静摩擦力为f，求：

（1）当kl＜f，对气缸缓慢加热到活塞移至缸筒口时，气缸内气体温度是多少？
（2）当kl＞f，对气缸缓慢加热到活塞移至缸筒口时，气缸内气体的温度又是多少？

如图所示，一足够高的直立气缸上端开口，用一个厚度不计的活塞封闭了一段高为90cm的气柱，活塞的横截面积为0.01m²，活塞与气缸间的摩擦不计，气缸侧壁通过一个密封接口与U形管相通，密封接口离气缸底部的高度为70cm，气缸与U形管相通处气体体积忽略不计．在图示状态时气体的温度为17℃，U形管两支管水银面的高度差h₁为6cm，右支管内水银面到管口的高度为20cm，大气压强p₀＝1.0×10⁵Pa保持不变，水银的密度ρ＝13.6×10³kg/m³．求：

（1）活塞的重力；
（2）现在将U形管右支管开口端用橡皮塞（厚度不计）封住，并在活塞上添加沙粒，同时对气缸内的气体缓缓加热，让活塞高度始终不变．当气体温度升高到57⁰C时，不再加沙粒，同时停止对气体加热，这时U形管两支管内水银面的高度差h₂变为多少？（气缸内气体温度变化不影响U形管）
（3）保持上题中的沙粒质量不变，让气缸内的气体逐渐冷却，那么当气体的温度至少降为多少^oC时，U形管内的水银开始流动？

如图，p-T和V-T图记录了一定质量的理想气体经历了温度从200K到600K缓慢升温过程的部分变化过程。试求：
① 温度为600K时气体的压强；
② 试在p-T图上将温度从400 K缓慢升高到600 K的过程用图线表示出来。

如图所示，竖直放置的圆筒形注射器，活塞上端接有气压表，能够方便测出所封闭理想气体的压强．开始时，活塞处于静止状态，此时气体体积为30cm³，气压表读数为1．l×10⁵Pa．若用力向下推动活塞，使活塞缓慢向下移动一段距离，稳定后气压表读数为2．2×10⁵Pa．不计活塞与气缸内壁间的摩擦，环境温度保持不变，

①简要说明活塞移动过程中，被封闭气体的吸放热情况；
① 求活塞稳定后气体的体积．

如图所示，用销钉固定的导热活塞把水平放置的导热气缸分隔成容积相同的两部分，分别封闭着A、B两部分理想气体：A部分气体压强为p_A0 = 2.5×10⁵ Pa，B部分气体压强为P_B0 = 1.5×10⁵ Pa。现拔去销钉，待活塞重新稳定后，(外界温度保持不变，活塞与气缸间摩擦可忽略不计，整个过程无漏气发生)

①求此时A部分气体体积与原来体积之比；
②判断此过程中A部分气体是吸热还是放热，并简述理由。

如图所示， 一密闭的截面积为S的圆筒形汽缸，高为H，中间有一薄活塞， 用一劲度系数为k的轻弹簧吊着，活塞重为G，与汽缸紧密接触不导热，若Ⅰ、Ⅱ气体是同种气体，且质量、温度、压强都相同时，活塞恰好位于汽缸的正中央，设活塞与汽缸壁间的摩擦可不计，汽缸内初始压强为p₀=1.0×10⁵Pa，温度为T₀， 求：

①弹簧原长．
②如果将汽缸倒置， 保持汽缸Ⅱ部分的温度不变，使汽缸Ⅰ部分升温，使得活塞在汽缸内的位置不变，则汽缸Ⅰ部分气体的温度升高多少?

如图所示，开口处有卡口、内截面积为S的圆柱形气缸开口向上竖直放置在水平面上，缸内总体积为V₀，大气压强为p₀，一厚度不计、质量为m的活塞（m＝0．2p₀S/g）封住一定量的理想气体，温度为T₀时缸内气体体积为0．8V₀，先在活塞上缓慢放上质量为2m的砂子，然后将缸内气体温度升高到2T₀，求：（1）初始时缸内气体的压强P₁ =?  （2）在活塞上放上质量为2m的砂子时缸内气体的体积V₂ =? （3）最后缸内气体的压强P₄=?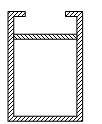

如图所示，一水平放置的气缸，由截面积不同的两圆筒连接而成，活塞A、B用一长为3L的刚性细杆连接，它们可以在筒内无摩擦地沿水平方向左右滑动．A、B的截面积分别为S_A=2S₀、S_B= S₀。A、B之间封闭着一定质量的理想气体．两活塞外侧（A的左方和B的右方）都是大气，大气压强始终保持为Po．活塞B的中心连一不能伸长的细线，细线的另一端固定在墙上，当气缸内气体温度为T₁=T₀，活塞A、B的平衡位置如图所示，此时细线中的张力为F₁= 0.2P₀S₀。（答案用已知量S₀、p₀、T₀表示）
（1）现使气缸内气体温度由初始温度T₁缓慢下降至T₂，T₂为多少时活塞开始向右移动？
（2）继续使气缸内气体温度缓慢下降至T₃，T₃为多少时活塞A刚刚右移到两圆筒连接处？
（3）活塞A移到两圆筒连接处之后，维持气体温度T₃不变，另外对B施加一个水平向左的推力，将两活塞慢慢推向左方，直到细线拉力重新变为F₁求此时的外加推力F是多大a

封闭在气缸内一定质量的理想气体由状态A变到状态D，其体积V与热力学温度关T系如图所示，该气体的摩尔质量为M，状态A的体积为V₀，温度为T₀，O、A、D三点在同一直线上，阿伏伽德罗常数为N_A。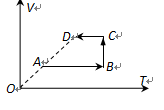

（1）由状态A变到状态D过程中     ▲      
A．气体从外界吸收热量，内能增加
B．气体体积增大，单位时间内与器壁单位面积碰撞的分子数减少
C．气体温度升高，每个气体分子的动能都会增大
D．气体的密度不变
（2）在上述过程中，气体对外做功为5J，内能增加9J，则气体    ▲  （选“吸收”或“放出”）热量  ▲  J。
（3）在状态D，该气体的密度为ρ，体积为2V₀，则状态D的温度为多少？该气体的分子数为多少？

一根两端开口、横截面积为S=2cm²足够长的玻璃管竖直插入水银槽中并固定（插入水银槽中的部分足够深）。管中有一个质量不计的光滑活塞，活塞下封闭着长L=21cm的气柱，气体的温度T₁=280K，外界大气压取P₀=1.0×10⁵Pa（相当于75cm汞柱高的压强）。

①对气体加热，使其温度升高到T₂=320K，求此时气柱的长度；
②在活塞上施加一个竖直向上的拉力F=4N，保持气体的温度T₂不变，求平衡后气柱的长度及此时管内外水银面的高度差。

如图所示，固定气缸两端活塞截面积分别为S₁和S₂，活塞间有轻杆相连，两活塞间为真空，摩擦不计。最初A内气体压强为p₀、体积为V₁、温度为T₁，B内气体体积为V₂、温度也为T₁。现将A内气体加热到T₂，B内气体温度始终保持不变，求：（1）活塞再达到平衡时移动的距离；（2）此时B中气体压强。

如图所示，两个可导热的气缸竖直放置，它们的底部由一细管连通（忽略细管的容积）。两气缸各有一活塞，质量分别为和，活塞与气缸壁无摩擦。活塞的下方为理想气体，上方为真空。当气体处于平衡状态时，两活塞位于同一高度。（已知=3,=2）

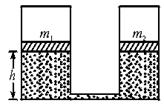
（1）在两活塞上同时各放一质量为的物块，求气体再次达到平衡后两活塞的高度差（假定环境的温度始终保持为）。
（2）在达到上一问的终态后，环境温度由缓慢上升到T，试问在这个过程中，气体对活塞做了多少功？气体是吸收还是放出了热量？（假定在气体状态变化过程中，两物块均不会碰到气缸顶部）

如图，一质量不计，可上下自由一点的活塞将圆筒分为上下两室，两室中分别封闭有理想气体，筒的侧壁为绝缘体，上底，下底及活塞均为导体并按图连接，活塞面积。在电键K断开时，两室中气体压强均为，间距，间距，将变阻器的滑片P滑到左端B，闭合电键后，活塞与下底分别带有等量异种电荷，并各自产生匀强电场，在电场力作用下活塞发生移动。稳定后，间距，间距，活塞D所带电流的绝对值(式中为与所带电荷产生的合场强，常量)求：

（1）两室中气体的压强（设活塞移动前后气体温度保持不变）；
（2）活塞受到的电场力大小F；
（3）所带电荷产生的场强大小和电源电压；
（4）使滑片缓慢地由向滑动，活塞如何运动，并说明理由。