高中物理理想气体的状态方程计算题

如图所示，在一个圆柱玻璃瓶中插入一根两端开口的玻璃管，接口处用蜡密封，圆柱玻璃瓶内有一部分水银封住密闭气体，管横截面积为S₁＝1 cm²、瓶的横截面积S₂＝6 cm²，细管内水银长度为h＝4 cm，封闭气体长度为L＝6 cm。大气压强为p₀＝76 cmHg，气体初始温度为T₁＝300 K，上管足够长。

①缓慢升高气体温度，求水银刚好全部进入玻璃管内时的温度T₂；
②若把温度升到427℃时，水银的下表面到瓶底的距离。

如图所示，透热的气缸内封有一定质量的理想气体，缸体质量M＝200kg，活塞质量m＝10kg，活塞面积S＝100cm²。活塞与气缸壁无摩擦且不漏气。此时，缸内气体的温度为27°C，活塞位于气缸正中，整个装置都静止。已知大气压恒为p₀＝1.0×10⁵P_a，重力加速度为g＝10m/s²。求：

（a）缸内气体的压强p₁；
（b）缸内气体的温度升高到多少°C时，活塞恰好会静止在气缸缸口AB处？

如图所示，为厚度和质量不计，横截面积为的绝热气缸倒扣在水平桌面上，气缸内有一绝热的“”型活塞固定在桌面上，活塞与气缸封闭一定质量的理想气体，开始时，气体的温度为，压强为，活塞与气缸底的距离为，活塞与气缸可无摩擦滑动且不漏气，大气压强为．求：

①此时桌面对气缸的作用力
②现通过电热丝给气体缓慢加热到，此过程中气体吸收热量为，内能增加了，
整过程活塞都在气缸内，求的值．

某教室的空间体积约为120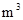．试计算在标准状况下，教室里空气分子数．已知：阿伏加德罗常数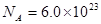mol ¹，标准状况下摩尔体积m³．（计算结果保留一位有效数字）

如图所示，一直立气缸由两个横截面积不同的圆筒连接而成，活塞A.B间封闭有一定质量的理想气体，A的上方和B的下方分别与大气相通。两活塞用长为L=30cm的不可伸长的细线相连，可在缸内无摩擦地上下滑动。当缸内封闭气体的温度为T₁=300K时，活塞A.B的平衡位置如图所示。已知活塞A.B的质量均为m=1.0kg，横截面积分别为S_A=20cm²、S_B=10cm²，大气压强为P₀=1.0×10⁵Pa，重力加速度为g=10m/s²。

（i）活塞A.B在图示位置时，求缸内封闭气体的压强；
（ii）现对缸内封闭气体缓慢加热，为使气缸不漏气，求缸内封闭气体的最高温度。

如图所示，在两端封闭粗细均匀的竖直长管道内，用一可自由移动的活塞A封闭体积相等的两部分气体。开始时管道内气体温度都为T₀ =" 500" K，下部分气体的压强p₀=1．25×10⁵ Pa，活塞质量m = 0．25 kg，管道的内径横截面积S =1cm²。现保持管道下部分气体温度不变，上部分气体温度缓慢降至T，最终管道内上部分气体体积变为原来的，若不计活塞与管道壁间的摩擦，g =" 10" m/s²，求此时上部分气体的温度T。

如图所示，在一端封闭的U形管中用水银柱封一段空气柱L，当空气柱的温度为7℃时，左臂水银柱的长度h₁=10cm，右臂水银柱长度h₂=7cm，气柱长度L=15cm；将U形管放入91℃水中且状态稳定时，左臂水银柱的长度变为7cm。求当时的大气压强（单位用cmHg）。

）（如图所示，水平放置一个长方体气缸，总体积为V，用无摩擦活塞（活塞绝热、体积不计）将内部封闭的理想气体分为完全相同的A、B两部分。初始时两部分气体压强均为P，温度均为T。若使A气体的温度升高，B气体的温度保持不变，求

(i)A气体的体积变为多少?
(ii)B气体在该过程中是放热还是吸热？

水深10m处有一无底铁箱倒扣在水底。且内部充满水，铁箱质量为560kg，容积为1m³，水温恒为7℃，同学们设计的打捞方案是用软管向铁箱内泵入空气，不计铁箱高度，厚度及泵入的空气质量，已知大气压恒为p₀=1atm=1.0×10⁵Pa，那么需要向铁箱内泵入多大体积的1atm、27℃的空气？（g=10m/s²）

如图所示，在两端封闭粗细均匀的竖直长管道内，用一可自由移动的活塞A封闭体积相等的两部分气体。开始时管道内气体温度都为T₀ =" 500" K，下部分气体的压强p₀=1．25×10⁵ Pa，活塞质量m = 0．25 kg，管道的内径横截面积S =1cm²。现保持管道下部分气体温度不变，上部分气体温度缓慢降至T，最终管道内上部分气体体积变为原来的，若不计活塞与管道壁间的摩擦，g =" 10" m/s²，求此时上部分气体的温度T。

如图所示，两端开口的气缸水平固定，A、B是两个厚度不计的活塞，可在气缸内无摩擦地滑动，其面积分别为S₁＝20cm²、S₂＝10cm²，它们之间用一根细杆连接，B通过水平细绳绕过光滑的定滑轮与质量为M＝2 kg的重物C连接，静止时气缸中气体的温度T₁＝600K，气缸两部分的气柱长均为L，已知大气压强p₀＝1×10⁵Pa，g取10m/s²，缸内气体可看作理想气体。

①求活塞静止时气缸内气体的压强；
②若降低气缸内气体的温度，当活塞A缓慢向右移动L时，求气缸内气体的温度。

(10分）如图，上粗下细且上端开口的薄壁玻璃管内有一部分水银封住密闭气体，横截面积分别为S₁＝1 cm²、S₂＝2 cm²，细管内水银长度为h₁＝4 cm，封闭气体长度为L＝6 cm。大气压强为p₀＝76 cmHg，气体初始温度为T₁＝280 K，上管足够长。

（1）缓慢升高气体温度，求水银刚好全部进入粗管内时的温度T₂；
（2）气体温度保持T₂不变，为使封闭气体长度变为8 cm，需向开口端注入的水银柱的体积为多少？

某同学在研究“一定质量气体体积不变时压强和温度关系”实验中，将气缸开口向上竖直放置在水平桌面上，在没有压强传感器的情况下，他将力传感器和活塞一起固定，测量活塞作用在传感器上沿竖直方向的力，如图A.所示。活塞的横截面积为S＝15 cm²，大气压强p₀＝1.0×10⁵ Pa，气缸质量M＝0.75 kg。当缸内气体温度t₁＝27 ℃时，力传感器示数恰好为零，升高气体的温度，根据测得数据作了如图B.所示的F﹣T图，忽略摩擦，取g＝10 m/s²。

（1）F＜0表明传感器对活塞的作用力方向为_______；
（2）直线的斜率为______，t₁温度时气体压强为______Pa；
（3）该同学又从t₁开始降低温度直至t₂＝﹣10 ℃进行实验，且操作无误，试在图B.中作出t₁至t₂温度区间内的F﹣T图线，并在坐标轴上注明必要数据。

两个相同的薄壁型气缸A和B，活塞的质量都为m，横截面积都为S，气缸的质量都为M，M/m＝3/2，气缸B的筒口处有卡环可以防止活塞离开气缸．将气缸B的活塞跟气缸A的气缸筒底用细线相连后，跨过定滑轮，气缸B放在倾角为光滑斜面上，气缸A倒扣在水平地面上，气缸A和B内装有相同质量的同种气体，体积都为V₀，温度都为T₀，如图所示，此时气缸A的气缸筒恰好对地面没有压力．设气缸内气体的质量远小于活塞的质量，大气对活塞的压力等于活塞重的1.5倍．

（1）若使气缸A的活塞对地面的压力为0，气缸A内气体的温度是多少？
（2）若使气缸B中的气体体积变为，气缸B内的气体的温度是多少？

如图所示，长为31cm、内径均匀的细玻璃管开口向上竖直放置，管内水银柱的上端正好与管口齐平，封闭气体的长为10cm，温度为27℃，外界大气压强不变。若把玻璃管在竖直平面内缓慢转至开口竖直向下，这时留在管内的水银柱长为15cm，然后再缓慢转回到开口竖直向上，求：

（1）大气压强的值；
（2）玻璃管重新回到开口竖直向上时空气柱的长度；
（3）当管内气体温度缓慢升高到多少℃时，水银柱的上端恰好重新与管口齐平？