高中物理平抛运动计算题

如图所示，滑板运动员从倾角为53°的斜坡顶端滑下，滑下的过程中他突然发现在斜面底端有一个高h="1.4" m、宽L="1.2" m的长方体障碍物，为了不触及这个障碍物，他必须在距水平地面高度H="3.2" m的A点沿水平方向跳起离开斜面（竖直方向的速度变为0）。已知运动员的滑板与斜面间的动摩擦因数μ=0.1，忽略空气阻力，重力加速度g取10m/s²。（已知sin53°=0.8，cos53°=0.6）求：

（1）运动员在斜面上滑行的加速度的大小；
（2）若运动员不触及障碍物，他从斜面上起跳后到落至水平面的过程所经历的时间；
（3）运动员为了不触及障碍物，他从A点沿水平方向起跳的最小速度。

如图所示，质量是1kg的小球用长为0.5 m的细线悬挂在O点，O点距地面高度为1m，如果使小球绕00′轴在水平面内做圆周运动，若细线最大承受拉力为12.5 N，(g=10m／s²).求：

(1)当小球的角速度为多大时，细线将断裂；
(2)线断裂后小球落地点与悬点的水平距离.

如图所示，水平轨道MN与竖直光滑半圆轨道相切于N点，轻弹簧左端固定在轨道的M点，将一质量为m=1kg的小物块靠在弹簧右端并压缩至O点，此时弹簧储有弹性势能E_p，现将小物块无初速释放，小物块恰能通过轨道最高点B，此后水平飞出再落回到水平面。已知ON的距离L=3.0m，小物块与水平轨道间的动摩擦因数μ=0.2，圆轨道半径R=0.4m，g取10 m/s²。求：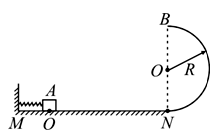

（1）小物块通过B点抛出后，落地点距N的水平距离x；
（2）弹簧储有的弹性势能E_p。

如图所示，质量为m的小球从A点水平抛出，抛出点距离地面高度为H，不计与空气的摩擦阻力，重力加速度为g。在无风情况下小球的落地点B到抛出点的水平距离为L；当有恒定的水平风力F时，小球仍以原初速度抛出，落地点C到抛出点的水平距离为3L/4，求：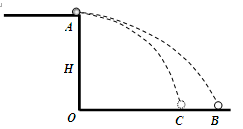

（1）小球初速度的大小； 
（2）水平风力F的大小；

如图为“快乐大冲关”节目中某个环节的示意图，参与游戏的选手会遇到一个人造山谷AOB，AO是高h＝3 m的竖直峭壁，OB是以A点为圆心的弧形坡，∠OAB＝60°，B点右侧是一段水平跑道．选手可以自A点借助绳索降到O点后再爬上跑道，但身体素质好的选手会选择自A点直接跃上跑道．选手可视为质点，忽略空气阻力，重力加速度g＝10 m/s²。

（1）若选手以速度v₀水平跳出后，能跳在水平跑道上，求v₀的最小值；
（2）若选手以速度v₁＝4 m/s水平跳出，求该选手在空中的运动时间。

某战士在倾角θ = 30°的山坡上进行投掷手榴弹训练。他从A点以某一初速度υ₀沿水平方向投出手榴弹，正好落在B点，测得AB 间的距离L= 90m。设空气阻力不计，取重力加速度g = 10m/s²。

（1）该型号手榴弹从拉动弦到爆炸需要T=5s的时间，若要求手榴弹正好落地爆炸，求战士从拉动弦到投出所用时间；
（2）求手榴弹抛出的初速度大小。

小明站在水平地面上，手握不可伸长的轻绳一端，绳的另一端系有质量为m的小球，甩动手腕，使球在竖直平面内做圆周运动，当球某次运动到最低点时，绳突然断掉，球飞行水平距离d后落地，如图所示，已知握绳的手离地面高度为d，手与球之间的绳长为，重力加速度为g，忽略手的运动半径和空气阻力。

①求绳断时球的速度大小和球落地时的速度大小 
②问绳能承受的最大拉力多大？
③改变绳长，使球重复上述运动，若绳仍在球运动到最低点时断掉，要使球抛出的水平距离最大，绳长应为多少？最大水平距离为多少？

如图所示，斜面AB倾角为θ=37°， 竖直圆弧轨道BC与斜面AB相切于B点，O点是圆弧轨道的圆心，OC一条竖直线，圆弧轨道的半径R=1m。一个质量M=10kg，从斜面底端A在恒力F的作用下，由静止开始沿斜面AB向上运动，当物体运动到B点时，撤去外力F后，物体沿着圆弧轨道运动，刚好通过圆弧上的C点，最后物体正好落在斜面底端A点。不计一切摩擦和空气阻力，重力加速度g=10m/s²。求：

（1）斜面AB的长度；
（2）恒力F的大小。

如图,在y>0的区域存在方向沿y轴负方向的匀强电场,场强大小为E，在y<0的区域存在方向垂直于xOy平面向外的匀强磁场。一个氕核 ¹ ₁H和一个氚核 ² ₁H先后从y轴上y=h点以相同的动能射出,速度方向沿x轴正方向。已知 ₁ ¹H进入磁场时,速度方向与x轴正方向的夹角为60°,并从坐标原点O处第一次射出磁场。 ₁ ¹H的质量为m,电荷量为q不计重力。求

（1） ₁ ¹H第一次进入磁场的位置到原点O的距离    

（2）磁场的磁感应强度大小    

（3） ₂ ¹H第一次离开磁场的位置到原点O的距离

某战士在倾角为30^o山坡上进行投掷手榴弹训练。他从A点以某一初速度v₀沿水平方向投出手榴弹，正好落在B点，测得AB=90m。若空气阻力不计，（g=10m/s²）求：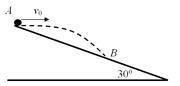

（1）手榴弹抛出的速度？
（2）从抛出开始经多长时间手榴弹与山坡间的距离最大？并求出此时手榴弹与山坡间的距离？

某人站在一平台上，用长L=0.6m的轻细线拴一个质量为m=0.6kg的小球，让它在竖直平面内以O点为圆心做圆周运动，当小球转到最高点A时，人突然撒手。经t=0.8s小球落地，落地点B与A点的水平距离x=4.8m，不计空气阻力，g=10m/s²。求：

（1）A点距地面高度h；
（2）人撒手前小球运动到A点时，绳对球的拉力F_T的大小。

一根长60cm的细绳，最多能承受100N的拉力，用它吊起一质量为4kg的物体，当物体摆动起来经过最低点时，绳子恰好被拉断。
（1）绳断时物体速度多大？
（2）若绳断处距离地面的高度为0.8m，求物体落地时的速度大小。（不计空气阻力，g=10m/s²）

如图所示，在粗糙水平台阶上放置一质量m=0.5kg的小物块，它与水平台阶间的动摩擦因数μ=0.5，与台阶边缘O点的距离s=5m。在台阶右侧固定一个圆弧挡板，圆弧半径R=1m，圆弧的圆心也在O点。今以O点为原点建立平面直角坐标系xOy。现用F=5N的水平恒力拉动小物块，一段时间后撤去拉力，小物块最终水平抛出并击中挡板。（，取g=10m/s²）

（1）若小物块恰能击中挡板上的P点（OP与水平方向夹角为37°），求其离开O点时的速度大小；
（2）为使小物块击中挡板，求拉力F作用的最短时间；
（3）改变拉力F的作用时间，使小物块击中挡板的不同位置，求击中挡板时小物块动能的最小值。

某水上游乐场举办了一场趣味水上比赛．如图所示，质量m=60kg的参赛者（可视为质点），在河岸上A点双手紧握一根长L=5.0m的不可伸长的轻绳，轻绳另一端系在距离水面高H=10.0m的O点，此时轻绳与竖直方向的夹角为θ=37°，C点是位于O点正下方水面上的一点，距离C点x=5.0m处的D点固定着一只救生圈，O、A、C、D各点均在同一竖直面内，若参赛者双手抓紧绳端点，从台阶上A点沿垂直于轻绳斜向下以一定的初速度跃出，当摆到O点正下方的B点时松开手，此后恰能落在救生圈内。（sin37°=0.6，cos37°=0.8， g=10m/s²）

（1）求参赛者经过B点时速度的大小v；
（2）求参赛者从台阶上A点跃出时的动能E_K；
（3）若手与绳之间的动摩擦因数为0.6，参赛者要顺利完成比赛，则每只手对绳的最大握力不得小于多少？（设最大静摩擦等于滑动摩擦力）

如图所示，质量为m的小球沿光滑的水平面冲上一光滑的半圆形轨道，轨道半径为R，小球在轨道最高点对轨道压力等于0.5mg，重力加速度为g，求：

（1）小球在最高点的速度大小；
（2）小球落地时，距最高点的水平位移大小；
（3）小球经过半圆轨道最低点时，对轨道的压力．