已知函数 .
.
(Ⅰ) ,使得函数
,使得函数 在
在 的切线斜率
的切线斜率 ,求实数
,求实数 的取值范围;
的取值范围;
(Ⅱ)求 的最小值.
的最小值.
已知函数 ,
, 为常数.
为常数.
(1)若函数 在
在 处的切线与
处的切线与 轴平行,求
轴平行,求 的值;
的值;
(2)当 时,试比较
时,试比较 与
与 的大小;
的大小;
(3)若函数 有两个零点
有两个零点 、
、 ,试证明
,试证明 .
.
设函数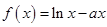 .
.
(1)当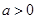 时,求函数
时,求函数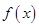 在区间
在区间 内的最大值;
内的最大值;
(2)当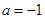 时,方程
时,方程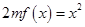 有唯一实数解,求正数
有唯一实数解,求正数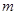 的值.
的值.
设
的导数
满足
,其中常数
.
(Ⅰ)求曲线
在点
处的切线方程.
(Ⅱ)设
.求函数
的极值.
已知曲线 :
:
(1)试求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)试求与直线 平行的曲线C的切线方程.
平行的曲线C的切线方程.
已知函数,
,其中
.
(Ⅰ)当时,求曲线
在点
处的切线方程;
(Ⅱ)当时,求
的单调区间;
(Ⅲ)证明:对任意的,
在区间
内均存在零点.
(本小题满分13分)已知函数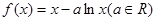 .
.
(1)当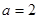 时,求曲线
时,求曲线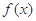 在
在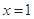 处的切线方程;
处的切线方程;
(2)设函数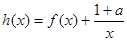 ,求函数
,求函数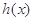 的单调区间;
的单调区间;
(3)若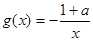 ,在
,在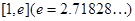 上存在一点
上存在一点 ,使得
,使得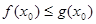 成立,求
成立,求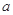 的取值范围.
的取值范围.
(本小题满分16分)已知函数 ,
, ,
, .
.
(1)若曲线 与直线
与直线 相切,求实数
相切,求实数 的值;
的值;
(2)记 ,求
,求 在
在 上的最大值;
上的最大值;
(3)当 时,试比较
时,试比较 与
与 的大小.
的大小.
已知函数f(x)=sinx,g(x)=mx-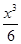 (m为实数).
(m为实数).
(1)求曲线y=f(x)在点P( ),f(
),f( )处的切线方程;
)处的切线方程;
(2)求函数g(x)的单调递减区间;
(3)若m=1,证明:当x>0时,f(x)<g(x)+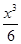 .
.