(本小题满分14分)设函数f(x)=(x–1)2+alnx,a∈R.
(Ⅰ)若曲线y=f(x)在点(1,f(1))处的切线与直线x+2y–1=0垂直,求a的值;
(Ⅱ)求函数f(x)的单调区间;
(Ⅲ)若函数f(x)有两个极值点x1,x2且x1<x2,求证:f(x2)>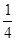 –
–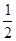 ln2.
ln2.
已知 的图像过原点,且在点
的图像过原点,且在点 处的切线与
处的切线与 轴平行,对任意
轴平行,对任意 ,都有
,都有 .
.
(1)求函数 在点
在点 处切线的斜率;
处切线的斜率;
(2)求 的解析式;
的解析式;
(3)设 ,对任意
,对任意 ,都有
,都有 .求实数
.求实数 的取值范围.
的取值范围.
(本小题满分14分)设函数 ,
,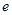 是自然对数的底数,
是自然对数的底数,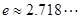 ,
,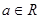 为常数.
为常数.
(1)若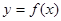 在
在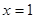 处的切线
处的切线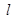 的斜率为
的斜率为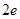 ,求
,求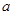 的值;
的值;
(2)在(1)的条件下,证明切线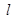 与曲线
与曲线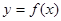 在区间
在区间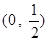 至少有1个公共点;
至少有1个公共点;
(3)若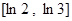 是
是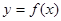 的一个单调区间,求
的一个单调区间,求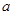 的取值范围.
的取值范围.
(本小题满分12分)已知函数 (
( 为自然对数的底数),曲线
为自然对数的底数),曲线 在点
在点 处的切线方程为
处的切线方程为 .
.
(1)求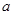 ,
, 的值;
的值;
(2)任意 ,
, 时,证明:
时,证明: .
.
(本小题满分12分)已知函数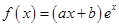 (
(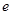 为自然对数的底数),曲线
为自然对数的底数),曲线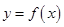 在点
在点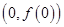 处的切线方程为
处的切线方程为 .
.
(1)求 ,
, 的值;
的值;
(2)任意 ,
, 时,证明:
时,证明: .
.
已知函数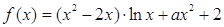 .
.
(1)当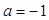 时,求
时,求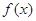 在
在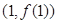 处的切线方程;
处的切线方程;
(2)设函数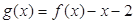 ,
,
(ⅰ)若函数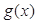 有且仅有一个零点时,求
有且仅有一个零点时,求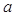 的值;
的值;
(ⅱ)在(ⅰ)的条件下,若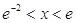 ,
, ,求
,求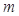 的取值范围。
的取值范围。
已知函数 的图象在
的图象在 处的切线方程为
处的切线方程为 ,其中有e为自然对数的底数。
,其中有e为自然对数的底数。
(1)求 的值;
的值;
(2)当 时,证明
时,证明 ;
;
(3)对于定义域为D的函数 若存在区间
若存在区间 时,使得
时,使得 时,
时, 的值域是
的值域是 。则称
。则称 是该函数
是该函数 的“保值区间”。设
的“保值区间”。设 +
+ ,问函数
,问函数 是否存在“保值区间”?若存在,求出一个“保值区间”,若不存在,说明理由。
是否存在“保值区间”?若存在,求出一个“保值区间”,若不存在,说明理由。
已知函数 在
在 处取得极值.
处取得极值.
(1)求a、b的值;
(2)求过点 且与曲线
且与曲线 相切的切线方程.
相切的切线方程.
已知函数
(Ⅰ)讨论函数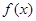 的单调性
的单调性
(Ⅱ)若函数 与函数
与函数 的图像关于原点对称且
的图像关于原点对称且 就函数
就函数 分别求解下面两问:
分别求解下面两问:
①问是否存在过点 的直线与函数
的直线与函数 的图象相切? 若存在,有多少条?若不存在,说明理由.
的图象相切? 若存在,有多少条?若不存在,说明理由.
②求证:对于任意正整数 ,均有
,均有 (
( 为自然对数的底数)
为自然对数的底数)
(本小题满分13分)已知函数 .
.
(1)若函数 的图象在
的图象在 处的切线斜率为1,求实数a的值;
处的切线斜率为1,求实数a的值;
(2)若函数 在
在 上是减函数,求实数a的取值范围.
上是减函数,求实数a的取值范围.
设函数 .
.
(1)若函数 在
在 处有极值,求函数
处有极值,求函数 的最大值;
的最大值;
(2)是否存在实数 ,使得关于
,使得关于 的不等式
的不等式 在
在 上恒成立?若存在,求出
上恒成立?若存在,求出 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
(3)证明:不等式 .
.
函数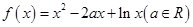 .
.
(I)函数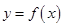 在点
在点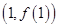 处的切线与直线
处的切线与直线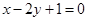 垂直,求a的值;
垂直,求a的值;
(II)讨论函数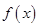 的单调性;
的单调性;
(III)不等式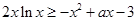 在区间
在区间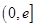 上恒成立,求实数a的取值范围.
上恒成立,求实数a的取值范围.
设 ,其中
,其中 为常数.
为常数.
(1)求曲线 (x)在点(4,2)处的切线方程;
(x)在点(4,2)处的切线方程;
(2)如果函数 (x)的图象也经过点(4,2),求
(x)的图象也经过点(4,2),求 (x)与(1)中的切线的交点.
(x)与(1)中的切线的交点.