高中数学组合几何解答题

已知函数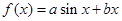的图像在点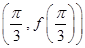处的切线方程为.
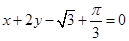（I）求实数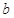，的值；
（Ⅱ）当时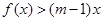，恒成立，求实数的取值范围.

设，其中，曲线在点处的切线垂直于轴.
（1）求的值；
（2）求函数的极值.

已知函数，其中.
（1）若，求曲线在点处的切线方程；
（2）求函数的极大值和极小值，若函数有三个零点，求的取值范围.

设二次函数的图像过原点，，的导函数为，且，
（1）求函数，的解析式；
（2）求的极小值；
（3）是否存在实常数和，使得和若存在，求出和的值；若不存在，说明理由.

已知函数
（Ⅰ）当时，求曲线在点处的切线方程；
（Ⅱ）求的单调区间；
（Ⅲ）若函数没有零点，求的取值范围.

设函数，曲线过点，且在点处的切线斜率为2．
(1)求a和b的值； (2)证明：．

已知函数在点处的切线方程为．
⑴求函数的解析式；
⑵若对于区间上任意两个自变量的值都有，求实数的最小值；
⑶若过点可作曲线的三条切线，求实数的取值范围．

设函数，曲线过点P（1，0），且在P点处的切斜线率为2．
（1）求，的值；
（2）证明：．

已知函数在点处的切线方程为．
（1）求，的值；
（2）对函数定义域内的任一个实数，恒成立，求实数的取值范围．

已知函数。
（Ⅰ）若,求函数的单调区间并比较与的大小关系
（Ⅱ）若函数的图象在点处的切线的倾斜角为，对于任意的，函数在区间上总不是单调函数，求的取值范围；
（Ⅲ）求证：。

已知函数.
（1）当时，求曲线在点处的切线方程；
（2）当，且，求函数的单调区间.

已知.
（1）当时，求曲线在点处的切线方程；
（2）若在处有极值，求的单调递增区间；
（3）是否存在实数，使在区间的最小值是3，若存在，求出的值；若不存在，说明理由.

设函数，，函数的图象与轴的交点也在函数的图象上，且在此点有公切线．
(Ⅰ)求，的值；
(Ⅱ)试比较与的大小．

已知函数，．
（Ⅰ）当时，求曲线在点处的切线方程；
（Ⅱ）若在区间上是减函数，求的取值范围．

设函数在处取得极值，且曲线在点处的切线垂直于直线．
（1）求的值；
（2）若函数，讨论的单调性．