定义方程f(x)= 的实数根x0叫做函数f(x)的“新驻点”,若函数g(x)=2x,h(x)=
的实数根x0叫做函数f(x)的“新驻点”,若函数g(x)=2x,h(x)= ,φ(x)=x3(x≠0)的“新驻点”分别为A,b,c,则A,b,c的大小关系为( )
,φ(x)=x3(x≠0)的“新驻点”分别为A,b,c,则A,b,c的大小关系为( )
A. |
B. |
C. |
D. |
设函数 是
是 上以4为周期的可导偶函数,则曲线
上以4为周期的可导偶函数,则曲线 在
在 处的切线的斜率为( )
处的切线的斜率为( )
A. |
B. |
C. |
D.4 |
设函数 的导函数为
的导函数为 ,那么下列说法正确的是( )
,那么下列说法正确的是( )
A.若 ,则 ,则 是函数 是函数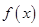 的极值点 的极值点 |
B.若 是函数 是函数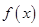 的极值点,则 的极值点,则 |
C.若 是函数 是函数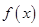 的极值点,则 的极值点,则 可能不存在 可能不存在 |
D.若 无实根 ,则函数 无实根 ,则函数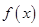 必无极值点 必无极值点 |
已知函数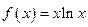 .若直线l过点(0,-1),并且与曲线y=f(x)相切,则直线l的方程为( )
.若直线l过点(0,-1),并且与曲线y=f(x)相切,则直线l的方程为( )
| A.x+y-1=0 |
| B.x-y-1=0 |
| C.x+y+1=0 |
| D.x-y+1=0 |
若点P是曲线 上任意一点,则点P到直线y=x-2的最小值为( ).
上任意一点,则点P到直线y=x-2的最小值为( ).
| A.1 |
B. |
C.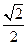 |
D.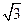 |
已知函数f(x)在R上满足f(x)=2f(2-x)-x2+8x-8,则曲线y=f(x)在点(1,f(1))处的切线方程是( )
| A.y=2x-1 | B.y=x | C.y=3x-2 | D.y=-2x+3 |