下列四个命题中,真命题的序号有 .(写出所有真命题的序号)
①若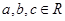 ,则“
,则“ ”是“
”是“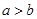 ”成立的充分不必要条件;
”成立的充分不必要条件;
②命题“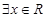 使得
使得 ”的否定是“
”的否定是“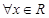 均有
均有 ”;
”;
③命题“若 ,则
,则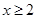 或
或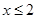 ”的否命题是“若
”的否命题是“若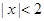 ,则
,则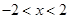 ”;
”;
④函数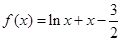 在区间
在区间 上有且仅有一个零点.
上有且仅有一个零点.
下列结论中正确的是 (填上所有正确结论得序号)
(填上所有正确结论得序号)
①对于函数 ,若
,若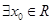 ,使得
,使得 ,则函数
,则函数 关于直线
关于直线 对称;
对称;
②函数 有2个零点;
有2个零点;
③若关于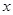 的不等式
的不等式 的解集为
的解集为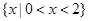 ,则
,则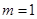 ;
;
④已知随机变量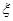 服从正态分布
服从正态分布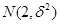 且
且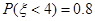 ,则
,则 ;
;
⑤等比数列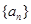 的前
的前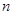 项和为
项和为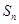 ,已知
,已知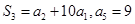 ,则
,则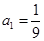
设直角三角形的两条直角边的长分别为 ,b,斜边长为c,斜边上的高为h,则有
,b,斜边长为c,斜边上的高为h,则有
① , ②
, ② ,
,
③ , ④
, ④ .
.
其中正确结论的序号是 ;进一步类比得到的一般结论是 .
下列命题:
① 动点M到两定点A、B的距离之比为常数 (
( 且
且 ),则动点M的轨迹是圆;
),则动点M的轨迹是圆;
② 椭圆 (
( )的离心率是
)的离心率是 ,则
,则 (
( 是椭圆的半焦距);
是椭圆的半焦距);
③ 双曲线 (
(
 )的焦点到渐近线的距离是
)的焦点到渐近线的距离是 ;
;
④ 已知抛物线 上有两个点A
上有两个点A ,B
,B ,且OA⊥OB(O是坐标原点),则
,且OA⊥OB(O是坐标原点),则 .
.
以上命题正确的是__________(写出所有正确结论的序号)
给出下列四个命题:
①命题“∀x∈R,cos x>0”的否定是:“∃x∈R,cos x≤0”;
②若lga+lgb=lg(a+b),则a+b的最大值为4;
③定义在R上的奇函数f(x)满足f(x+2)=-f(x),则f(6)的值为0;
④已知随机变量X服从正态分布N(1,σ2),P(X≤5)=0.81,则P(X≤-3)=0.19;其中真命题的序号是________.
定义平面向量的一种运算:a b=|a||b|sin 〈a,b〉,则下列命题:①a
b=|a||b|sin 〈a,b〉,则下列命题:①a b=b
b=b a;②λ(a
a;②λ(a b)=(λa)
b)=(λa)  b;③(a+b)c=(a
b;③(a+b)c=(a c)+(b
c)+(b c);④若a=(x1,y1),b=(x2,y2),则a
c);④若a=(x1,y1),b=(x2,y2),则a b=|x1y2-x2y1|.其中真命题是________________________(写出所有真命题的序号).
b=|x1y2-x2y1|.其中真命题是________________________(写出所有真命题的序号).
以下四个命题中:
①从匀速传递的产品生产流水线上,质检员每10分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
②两个随机变量的线性相关性越强,相关系数的绝对值越接近于1;
③某项测量结果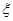 服从正太态布
服从正太态布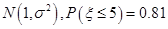 ,则
,则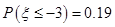 ;
;
④对于两个分类变量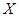 和
和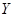 的随机变量
的随机变量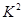 的观测值
的观测值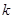 来说,
来说,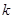 越小,判断“
越小,判断“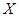 与
与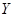 有关系”的把握程度越大.
有关系”的把握程度越大.
以上命题中其中真命题的个数为 .
给出下列命题:
①函数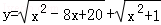 的最小值为5;
的最小值为5;
②若直线y=kx+1与曲线y=|x|有两个交点,则k的取值范围是﹣1≤k≤1;
③若直线m被两平行线l1:x﹣y+1=0与l2:x﹣y+3=0所截得的线段的长为2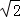 ,则m的倾斜角可以是15°或75°
,则m的倾斜角可以是15°或75°
④设Sn是公差为d(d≠0)的无穷等差数列{an}的前n项和,若对任意n∈N*,均有Sn>0,则数列{Sn}是递增数列
⑤设△ABC的内角A.B.C所对的边分别为a,b,c,若三边的长为连续的三个正整数,且A>B>C,3b=20acosA则sinA:sinB:sinC为6:5:4
其中所有正确命题的序号是 .
下列说法:①“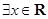 ,
,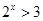 ”的否定是“
”的否定是“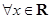 ,
,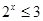 ”;②函数
”;②函数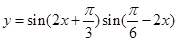 的最小正周期是
的最小正周期是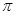 ;③命题“函数
;③命题“函数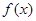 在
在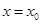 处有极值,则
处有极值,则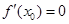 ”的否命题是真命题;④
”的否命题是真命题;④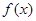 是
是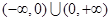 上的奇函数,
上的奇函数,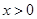 的解析式是
的解析式是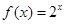 ,则
,则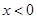 时的解析式为
时的解析式为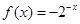 .其中正确的说法是__________.
.其中正确的说法是__________.