设 为不小于2的正整数,对任意
为不小于2的正整数,对任意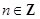 ,若
,若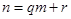 (其中
(其中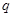 ,
,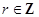 ,且
,且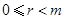 ),则记
),则记 ,如
,如 ,
, .下列关于该映射
.下列关于该映射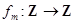 的命题中,正确的是 .
的命题中,正确的是 .
①若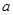 ,
,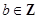 ,则
,则
②若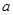 ,
, ,
,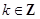 ,且
,且 ,则
,则
③若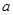 ,
, ,
,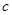 ,
, ,且
,且 ,
, ,则
,则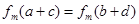
④若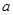 ,
, ,
,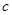 ,
, ,且
,且 ,
, ,则
,则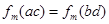 .
.
下列四个命题中,真命题的序号有 .(写出所有真命题的序号)
①若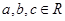 ,则“
,则“ ”是“
”是“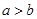 ”成立的充分不必要条件;
”成立的充分不必要条件;
②命题“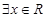 使得
使得 ”的否定是“
”的否定是“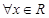 均有
均有 ”;
”;
③命题“若 ,则
,则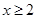 或
或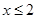 ”的否命题是“若
”的否命题是“若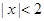 ,则
,则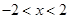 ”;
”;
④函数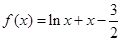 在区间
在区间 上有且仅有一个零点.
上有且仅有一个零点.
给出下列四个命题:
①命题 的否定是
的否定是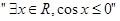 ;
;
②函数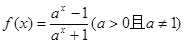 在
在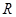 上单调递减;
上单调递减;
③设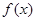 是
是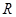 上的任意函数, 则
上的任意函数, 则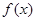 |
|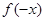 | 是奇函数,
| 是奇函数,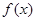 +
+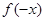 是偶函数;
是偶函数;
④定义在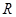 上的函数
上的函数 对于任意
对于任意 的都有
的都有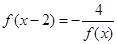 ,则
,则 为周期函数;
为周期函数;
⑤命题p: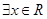 ,
,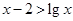 ;命题q:
;命题q: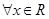 ,
,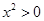 .则命题
.则命题 是真命题;
是真命题;
其中真命题的序号是 (把所有真命题的序号都填上).
以 表示值域为
表示值域为 的函数组成的集合,
的函数组成的集合, 表示具有如下性质的函数
表示具有如下性质的函数 组成的集合:对于函数
组成的集合:对于函数 ,存在一个正数
,存在一个正数 ,使得函数
,使得函数 的值域包含于区间
的值域包含于区间 .例如,当
.例如,当 ,
, 时,
时, ,
, .现有如下命题:
.现有如下命题:
①设函数 的定义域为
的定义域为 ,则“
,则“ ”的充要条件是“
”的充要条件是“ ,
, ,
, ”;
”;
②函数 的充要条件是
的充要条件是 有最大值和最小值;
有最大值和最小值;
③若函数 ,
, 的定义域相同,且
的定义域相同,且 ,
, ,则
,则 ;
;
④若函数 (
( ,
, )有最大值,则
)有最大值,则 .
.
其中的真命题有 (写出所有真命题的序号)
下列说法正确的是 .(填上所有正确答案的序号)
①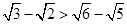 ;
;
② 任何集合都有子集;
③ 实数没有共轭复数;
④ 命题“正三角形的三条边全相等.”的逆否命题是“如果一个三角形的三条边全不相等,那么这个三角形不是正三角形.”
给出以下四个命题:
①命题 ;命题
;命题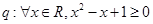 .则命题“
.则命题“ 且
且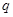 ”是真命题;
”是真命题;
②求函数 的零点个数为3;
的零点个数为3;
③函数 (
(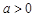 且
且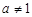 )与函数
)与函数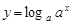 (
(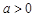 且
且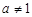 )的定义域相同;
)的定义域相同;
④函数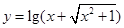 是奇函数.
是奇函数.
其中不正确的命题序号是__________(把你认为不正确的命题序号都填上).
下列4个命题:
①“如果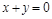 ,则
,则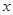 、
、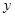 互为相反数”的逆命题
互为相反数”的逆命题
②“如果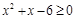 ,则
,则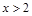 ”的否命题
”的否命题
③在△ABC中,“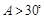 ”是“
”是“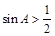 ”的充分不必要条件
”的充分不必要条件
④“函数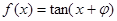 为奇函数”的充要条件是“
为奇函数”的充要条件是“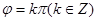 ”
”
其中真命题的序号是 .
若命题“存在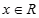 ,使得
,使得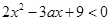 成立”为假命题,则实数
成立”为假命题,则实数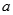 的取值范围是 .
的取值范围是 .
设非空集合 ,若对
,若对 中任意两个元素
中任意两个元素 ,
,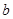 ,通过某个法则“
,通过某个法则“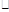 ”,使
”,使 中有唯一确定的元素
中有唯一确定的元素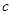 与之对应,则称法则“
与之对应,则称法则“ ”为集合
”为集合 上的一个代数运算。若
上的一个代数运算。若 上的代数运算“
上的代数运算“ ”还满足:(1)对
”还满足:(1)对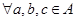 ,都有
,都有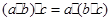 ;(2)对
;(2)对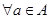 ,
,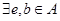 ,使得
,使得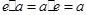 ,
,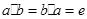 。称
。称 关于法则“
关于法则“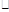 ”构成一个群。给出下列命题:
”构成一个群。给出下列命题:
①实数的除法是实数集上的一个代数运算;
②自然数集关于自然数的加法不能构成一个群;
③非零有理数集关于有理数的乘法构成一个群;
④正整数集关于法则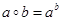 构成一个群。
构成一个群。
其中正确命题的序号是____________。(填上所有正确命题的序号)。