以 表示值域为
表示值域为 的函数组成的集合,
的函数组成的集合, 表示具有如下性质的函数
表示具有如下性质的函数 组成的集合:对于函数
组成的集合:对于函数 ,存在一个正数
,存在一个正数 ,使得函数
,使得函数 的值域包含于区间
的值域包含于区间 .例如,当
.例如,当 ,
, 时,
时, ,
, .现有如下命题:
.现有如下命题:
①设函数 的定义域为
的定义域为 ,则“
,则“ ”的充要条件是“
”的充要条件是“ ,
, ,
, ”;
”;
②函数 的充要条件是
的充要条件是 有最大值和最小值;
有最大值和最小值;
③若函数 ,
, 的定义域相同,且
的定义域相同,且 ,
, ,则
,则 ;
;
④若函数 (
( ,
, )有最大值,则
)有最大值,则 .
.
其中的真命题有 (写出所有真命题的序号)
函数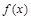 的定义域为A,若
的定义域为A,若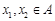 且
且 时总有
时总有 ,则称
,则称 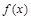 为单函数.例如,函数
为单函数.例如,函数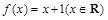 是单函数.下列命题:
是单函数.下列命题:
①函数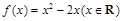 是单函数;②函数
是单函数;②函数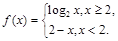 是单函数;
是单函数;
③若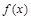 为单函数,
为单函数, 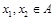 且
且 ,则
,则 ;
;
④若函数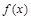 在定义域内某个区间D上具有单调性,则
在定义域内某个区间D上具有单调性,则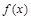 一定是单函数.
一定是单函数.
其中真命题是 (写出所有真命题的编号).
设命题p:非零向量a,b,|a|=|b|是(a+b)⊥(a-b)的充要条件;命题q:平面上M为一动点,A,B,C三点共线的充要条件是存在角α,使 =sin2α
=sin2α +cos2α
+cos2α ,下列命题①p∧q;②p∨q;③¬p∧q;④¬p∨q.
,下列命题①p∧q;②p∨q;③¬p∧q;④¬p∨q.
其中假命题的序号是________.(将所有假命题的序号都填上)
给出以下四个命题:
①已知命题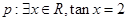 ;命题
;命题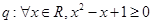 .则命题
.则命题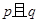 是真命题;
是真命题;
②命题“若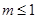 ,则
,则 有实根”的逆否命题;
有实根”的逆否命题;
③命题“面积相等的三角形全等”的否命题;
④命题 的逆命题.
的逆命题.
其中正确命题的序号为___________.(把你认为正确的命题序号都填上)
关于函数 有下列命题:①函数
有下列命题:①函数 的图像关于y轴对称;②在区间(-∞,0)上,函数
的图像关于y轴对称;②在区间(-∞,0)上,函数 是减函数;③函数
是减函数;③函数 的最小值为lg2;④在区间(1,+∞)上,函数
的最小值为lg2;④在区间(1,+∞)上,函数 是增函数。其中是真命题的序号为 。
是增函数。其中是真命题的序号为 。
给出以下四个命题:
①为了解600名学生对学校某项教改试验的意见,打算从中抽取一个容量为30的样本,考虑用系统抽样,则分段的间隔k为30;
②已知 是空间四点,命题甲:
是空间四点,命题甲: 四点不共面,命题乙:直线
四点不共面,命题乙:直线 和
和 不相交,则甲是乙成立的充分不必要条件;
不相交,则甲是乙成立的充分不必要条件;
③对分类变量X与Y的随机变量k2的观测值k来说,k越小,判断“X与Y有关系”的把握程度越大.
④若双曲线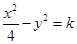 的渐近线方程为
的渐近线方程为 ,则k=1.其中真命题的序号是 .
,则k=1.其中真命题的序号是 .
定义在 上的函数
上的函数 ,其图象是连续不断的,如果存在非零常数
,其图象是连续不断的,如果存在非零常数 (
( ),使得对任意的
),使得对任意的 ,都有
,都有 ,则称
,则称 为“倍增函数”,
为“倍增函数”, 为“倍增系数”,
为“倍增系数”,
下列命题为真命题的是_ __(写出所有真命题对应的序号).
①若函数 是倍增系数
是倍增系数 的倍增函数,则
的倍增函数,则 至少有1个零点;
至少有1个零点;
②函数 是倍增函数,且倍增系数
是倍增函数,且倍增系数 ;
;
③函数 是倍增函数,且倍增系数
是倍增函数,且倍增系数 ;
;
④ .
.
下列说法正确的是 .(填上所有正确答案的序号)
①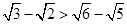 ;
;
② 任何集合都有子集;
③ 实数没有共轭复数;
④ 命题“正三角形的三条边全相等.”的逆否命题是“如果一个三角形的三条边全不相等,那么这个三角形不是正三角形.”
下列4个命题:
①“如果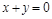 ,则
,则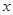 、
、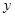 互为相反数”的逆命题
互为相反数”的逆命题
②“如果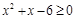 ,则
,则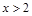 ”的否命题
”的否命题
③在△ABC中,“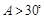 ”是“
”是“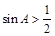 ”的充分不必要条件
”的充分不必要条件
④“函数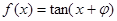 为奇函数”的充要条件是“
为奇函数”的充要条件是“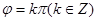 ”
”
其中真命题的序号是 .
若命题“存在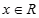 ,使得
,使得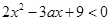 成立”为假命题,则实数
成立”为假命题,则实数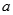 的取值范围是 .
的取值范围是 .