设 是两条直线,
是两条直线, 是两个平面,则下列4组条件中所有能推得
是两个平面,则下列4组条件中所有能推得 的条件是 。(填序号)
的条件是 。(填序号)
①
 ∥
∥ ,
, ;②
;② ;
;
③
 ,
, ∥
∥ ;④
;④ ,
, ∥
∥ ,
, ∥
∥ 。
。
.连接球面上两点的线段称为球的弦,半径为4的球的两条弦AB、CD的长度分别为2和4,M、N分别是AB、CD的中点,两条弦的两端都在球面上运动,有下面四个命题:
①弦AB、CD可能相交于点M;
②弦AB、CD可能相交于点N;
③MN的最大值是5;
④MN的最小值是1;
其中所有正确命题的序号为 .
给出下列四个命题:
(1)当 时,有
时,有 ≥2
≥2
(2)圆 上任意一点M关于直线
上任意一点M关于直线 的对称点
的对称点 也在该圆上。
也在该圆上。
(3)若函数 的图象关于
的图象关于 对称,则
对称,则 为偶函数。
为偶函数。
(4)函数 与函数
与函数 的图象关于直线
的图象关于直线 对称
对称
其中正确命题的序号为______________________________.
如图,边长为a的正△ABC的中 线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有 (只需填上正确命题的序号).
线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有 (只需填上正确命题的序号).
①动点A′在平面ABC上的射影在线段AF上;
②三棱锥A′—FED的体积有最大值;
③恒有平面A′GF⊥平面BCED;
④异面直线A′E与BD不可能互相垂直;
⑤异面直线FE与A′D所成角的取值范围是 .
.
从正方体的八个顶点中任意选择4个顶点,它们可能是如下几种几何体(或平面图形)的4个顶点,这些几何体(或平面图形)是___________(写出所有正确的结论的编号)
①矩形
②不是矩形的平行四边形
③有三个面为等腰直角三角形,有一个面为等边三角形的四面体
④每个面都是等边三角形的四面体
下列正确结论的序号是
①命题
②命题“若 ”的否命题是“
”的否命题是“ ”
”
③已知线性回归方程是 则当自变量的值为2时,因变量的精确值为7;
则当自变量的值为2时,因变量的精确值为7;
④若 ,则不等式
,则不等式 成立的概率是
成立的概率是 .
.
下列说法:
①已知 则
则 方向上的投影为
方向上的投影为 ;
;
②关于 的不等式
的不等式 恒成立,则
恒成立,则 的取值范围是
的取值范围是 ;
;
③函数 为奇函数的充要条件是
为奇函数的充要条件是 ;
;
④将函数 图像向右平移
图像向右平移 个单位,得到函数
个单位,得到函数 的图像
的图像
其中正确的命题序号是 (填出所有正确命题的序号)。
在 中,角A,B,C所对应的边分别是a,b,c,已知
中,角A,B,C所对应的边分别是a,b,c,已知 ,给出下列结论
,给出下列结论
① 的边长可以组成等差数列
的边长可以组成等差数列 
 ④若b+c=8,则
④若b+c=8,则 的面积是
的面积是 其中正确的结论序号是 .
其中正确的结论序号是 .
给出以下4个命题:
①曲线 按
按 平移可得曲线
平移可得曲线 ;
;
②若|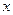 -1|+|
-1|+| -1|
-1| ,则使
,则使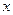

 取得最小值的最优解有无数多个;
取得最小值的最优解有无数多个;
③设 、
、 为两个定点,
为两个定点,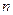 为
为 常数,
常数, ,则动点
,则动点 的轨迹为双曲线;
的轨迹为双曲线;
④若椭圆的左、右焦点分别为 、
、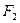 ,
, 是该椭圆上的任意一点,延长
是该椭圆上的任意一点,延长 到点
到点 ,使
,使 ,则点
,则点 的轨迹是圆.
的轨迹是圆.
其中所有真命题的序号为 .
.定义在实数集R上的函数 ,如果存在函数
,如果存在函数 (A、B为常数),使得
(A、B为常数),使得 对一切实数
对一切实数 都
都 成立,那么称
成立,那么称 为函数
为函数 的一个承托函数。给出如下四个命题:①对于给定的函数
的一个承托函数。给出如下四个命题:①对于给定的函数 ,其承托函数可能不存在,也可能有无数个;②定义域和值域都是R的函数
,其承托函数可能不存在,也可能有无数个;②定义域和值域都是R的函数 不存在承托函数;③
不存在承托函数;③ 为函数
为函数 的一个承托函数;④
的一个承托函数;④ 为函数
为函数 的一个承托函数。其中正确的命题有 。
的一个承托函数。其中正确的命题有 。
已知两条不同的直线 和平面
和平面 .给出下面三个命题:
.给出下面三个命题:
① ,
,
 ;②
;② ,
,
 ;③
;③ ,
,
 .
. 其中真命题的序号有 .(写出你认为所有真命题的序号)
其中真命题的序号有 .(写出你认为所有真命题的序号)
给出下列 关于互不相同的直线m,n,l和平面
关于互不相同的直线m,n,l和平面 的四个命题:
的四个命题:
①  不共面;
不共面;
② l、m是异面直线, ;
;
③ 若 ;
;
④ 若
其中假命题是 。
下列四个命题:
①m= 是两直线2x+my十1=0与mx+y-1=0平行的充分必要条件;②直线
是两直线2x+my十1=0与mx+y-1=0平行的充分必要条件;②直线 与圆
与圆 恒有公共点。③当
恒有公共点。③当 ;④一椭圆内切于长为6,宽为2的矩形,在矩形内随机地撒300颗黄豆,数得落在椭圆外的黄豆数为96
;④一椭圆内切于长为6,宽为2的矩形,在矩形内随机地撒300颗黄豆,数得落在椭圆外的黄豆数为96
颗,以此实验数据为依据可以估算出椭圆的面积约为 8.16。
正确命题的序号为 (写出所有正确命题的序号)
、给出下列五个命题:①不等式 的解集为
的解集为 ;②若函数
;②若函数 为偶函数,则
为偶函数,则 的图象关于
的图象关于 对称;③若不等式
对称;③若不等式 的解集为空集,必有
的解集为空集,必有 ;④函数
;④函数 的图像与直线
的图像与直线 至多有一个交点。其中所有正确命题的序号是______________
至多有一个交点。其中所有正确命题的序号是______________