设命题p:关于x的不等式2|x-2|<a的解集为;命题q:函数y=lg(ax2-x+a)的值域是R.如果命题p和q有且仅有一个正确,求实数a的取值范围.
已知命题p:函数y=loga(1-2x)在定义域上单调递增;命题q:不等式(a-2)x2+2(a-2)x-4<0对任意实数x恒成立.若p∨q是真命题,求实数a的取值范围.
已知命题p:方程2x2+ax-a2=0在[-1,1]上有解;命题q:只有一个实数x满足不等式x2+2ax+2a≤0,若命题“p∨q”是假命题,求a的取值范围.
设命题p:函数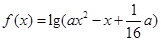 的定义域为R;命题q:不等式
的定义域为R;命题q:不等式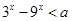 对一切实数均成立。
对一切实数均成立。
(1)如果p是真命题,求实数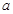 的取值范围;
的取值范围;
(2)如果命题“p或q”为真命题,且“p且q”为假命题,求实数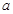 的取值范围。
的取值范围。
已知函数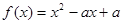 .设
.设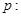 方程
方程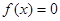 有实数根;
有实数根;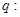 函数
函数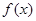 在区间
在区间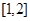 上是增函数.若
上是增函数.若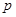 和
和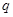 有且只有一个正确,求实数
有且只有一个正确,求实数 的取值范围.
的取值范围.
已知命题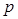 :方程
:方程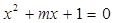 有两个不等的负实根,命题
有两个不等的负实根,命题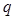 :方程
:方程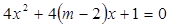 无实根.若
无实根.若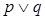 为真,
为真,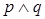 为假,求实数
为假,求实数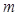 的取值范围.
的取值范围.
设命题 :方程
:方程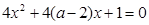 无实数根;命题
无实数根;命题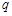 :函数
:函数 的值域是
的值域是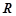 .如果命题
.如果命题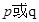 为真命题,
为真命题, 为假命题,求实数
为假命题,求实数 的取值范围。
的取值范围。