证明:三角形ABC三个内角成等差数列的充要条件是有一个内角为 .
.
(本小题满分14分)
已知命题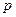 :方程
:方程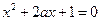 有两个不相等的负实数根;命题
有两个不相等的负实数根;命题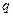 :函数
:函数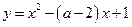 无零点.
无零点.
(1)若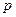 为真命题,求实数
为真命题,求实数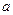 的取值范围;
的取值范围;
(2)若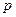 或
或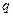 为真,
为真,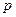 且
且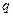 为假,求实数
为假,求实数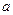 的值的集合.
的值的集合.
已知命题 命题
命题 使
使 ,
,
若命题“ 且
且 ”是假命题,命题“
”是假命题,命题“ 或
或 ”是真命题,求实数
”是真命题,求实数 的取值范围.
的取值范围.
已知数列{an}、{bn}满足:a1=1,a2=a(a为实数),且 ,其中n=1,2,3,…
,其中n=1,2,3,…
(Ⅰ)求证:“若数列{an}是等比数列,则数列{bn}也是等比数列”是真命题;
(Ⅱ)写出(Ⅰ)中命题的逆命题;判断它是真命题还是假命题,并说明理由.
分别写出下列命题的逆命题、否命题、逆否命题,并判断它们的真假。
(1)若q<1,则方程x2+2x+q=0有实根;
(2)若ab=0,则a=0或b=0;
(3)若x2+y2=0,则x、y全为零;
(4)如果两圆外切,那么圆心距等于两圆半径之和;
(5)奇数不能被2整除。
已知条件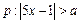 和条件
和条件 ,现在要选择适当的实数
,现在要选择适当的实数 的值,分别利用所给的两上条件作为
的值,分别利用所给的两上条件作为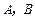 构造命题:“若
构造命题:“若 则
则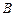 ”,并使得构造的原命题为真命题,而其逆命题为假命题,则这样的一个原命题可以是什么?并说明为什么这一命题是符合要求的命题.
”,并使得构造的原命题为真命题,而其逆命题为假命题,则这样的一个原命题可以是什么?并说明为什么这一命题是符合要求的命题.
现有命题:若 ,且
,且 的两个区间
的两个区间 上都是增函数,由
上都是增函数,由 在集合
在集合 ,若认为该命题为真,请给出证明;若认为该命题为假,请对原命题予以补充条件,使原命题能成立;先写出补充条件,然后证明给出的真命题.
,若认为该命题为真,请给出证明;若认为该命题为假,请对原命题予以补充条件,使原命题能成立;先写出补充条件,然后证明给出的真命题.