设 是两个不同的平面,
是两个不同的平面, 是一条直线,以下命题正确的是
是一条直线,以下命题正确的是
A.若 ,则 ,则 |
B.若 ,则 ,则 |
C. 若 若 ,则 ,则 |
D.若 ,则 ,则 |
定义平面向量之间的一种运算“*”如下:对任意的 ,令
,令 。给出以下四个命题:(1)若
。给出以下四个命题:(1)若 与
与 共线,则
共线,则 ;(2)
;(2) ;(3)对任意的
;(3)对任意的 ,有
,有 ;(4)
;(4) 。(注:这里
。(注:这里 指
指 与
与 的数量积)则其中所有真命题的序号是()
的数量积)则其中所有真命题的序号是()
| A.(1)(2)(3) | B.(2)(3)(4) | C.(1)(3)(4) | D.(1)(2)(4) |
设 是三条不同的直线,
是三条不同的直线, 是两个不同的平面,则
是两个不同的平面,则 的一个充分条件为( )
的一个充分条件为( )
A. |
B. |
C. |
D. |
给出定义:若 (其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m在此基础上给出下列关于函数
(其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m在此基础上给出下列关于函数 的四个命题:
的四个命题:
① ②
②
③ ④
④ 的定义域为R,值域是
的定义域为R,值域是
则其中真命题的序号是 ( )
| A.①② | B.①③ | C.②④ | D.③④ |
第Ⅱ卷
下列有关命题的说法正确的是 ( )
A.命题“若 ”的否定命题为“若 ”的否定命题为“若 ” ” |
B.“ ”是“ ”是“ ”的必要而不充分条件 ”的必要而不充分条件 |
C.命题“ ”的否定是“ ”的否定是“ ” ” |
D.命题“若 ”的逆否定命题为真命题。 ”的逆否定命题为真命题。 |
下列四个命题:
① 的展开式共有6项;
的展开式共有6项;
②设回归直线方程为 =2-2.5x,当变量x增加—个单位时,y平均增加2.5个单位
=2-2.5x,当变量x增加—个单位时,y平均增加2.5个单位 ;
;
③已知ξ服从正态分布N (0, ),且P(-2≤ξ≤0)=0.4,则P(ξ>2)=0.2;
),且P(-2≤ξ≤0)=0.4,则P(ξ>2)=0.2;
④已知函数f(a)= ,则f[f(
,则f[f( )]=1-cos1.其中正确命题的个数为
)]=1-cos1.其中正确命题的个数为
| A.4 | B.3 | C.2 | D.1 |
已知各项均不为零的数列{ },定义向量
},定义向量 =(
=( ,
,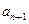 ),
),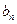 =(n,n+1),n∈N﹡,下列命题中真命题是
=(n,n+1),n∈N﹡,下列命题中真命题是
A.若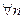 ∈N﹡,总有 ∈N﹡,总有 ∥ ∥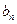 成立,则数列{ 成立,则数列{ }是等差数列 }是等差数列 |
B.若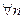 ∈N﹡总有 ∈N﹡总有 ∥ ∥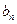 成立,则数列{ 成立,则数列{ }是等比数列 }是等比数列 |
C.若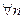 ∈N﹡总有 ∈N﹡总有 ⊥ ⊥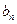 成立,则数列{ 成立,则数列{ }是等差数列 }是等差数列 |
D.若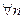 ∈N﹡总有 ∈N﹡总有 ⊥ ⊥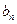 成立,则数列{ 成立,则数列{ }是等比数列 }是等比数列 |
下列命题错误的是
| A.命题“若lnx=0,则x=1”的逆否命题为“若x≠1,则lnx≠0” |
B.“x>2”是“ < <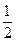 ”的充分不必要条件 ”的充分不必要条件 |
C.命题p: ∈R,使得sinx>1,则 ∈R,使得sinx>1,则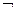 p: p: ∈R,均有sinx≤1 ∈R,均有sinx≤1 |
| D.若p∧q为假命题,则p,q均为假命题 |
已知直线m、n与平面α、β,下列命题正确的是 ( )
| A.m//α,n//β且α//β,则m//n | B. |
C. |
D. |
下列命题正确的是 ( )
A.命题 的否定是“ 的否定是“ ” ” |
B.已知 是“ 是“ ”的充分不必要条件 ”的充分不必要条件 |
C.已知线性回归方程是 ,当变量x的值为5时,其预报值为13 ,当变量x的值为5时,其预报值为13 |
D.若 ,则不等式 ,则不等式 成立的概率是 成立的概率是 |
给定下列四个命题:①若一个平面内的两条直线与另一个 平面都平行,那么这两个平面互相平行。②若一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。③垂直与同一直线的两条直线互相垂直。④若两个平面互相垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直。其中为真命题的是( )
平面都平行,那么这两个平面互相平行。②若一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。③垂直与同一直线的两条直线互相垂直。④若两个平面互相垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直。其中为真命题的是( )
| A.①和② | B.②和③ | C.②和④ | D.③和④ |
知 、
、 、
、 为互不重合的三个平面,命题
为互不重合的三个平面,命题 若
若 ,
, ,则
,则 ;命题
;命题 若
若 上不共线的三点到
上不共线的三点到 的距离相等,则
的距离相等,则 。对以上两个命题,下列结论中正确的是( )
。对以上两个命题,下列结论中正确的是( )
A.命题“ 且 且 ”为真 ”为真 |
B.命题“ 或 或 ”为假 ”为假 |
C.命题“ 或 或 ”为假 ”为假 |
D.命题“ 且 且 ”为假 ”为假 |