下列命题中错误的是:( )
A.如果α⊥β,那么α内一定存在直线平行于平面β ; ; |
| B.如果α⊥β,那么α内所有直线都垂直于平面β; |
| C.如果平面α不垂直平面β,那么α内一定不存在直线垂直于平面β; |
| D.如果α⊥γ,β⊥γ,α∩β=l,那么l⊥γ. |
下列命题为真命题的是( )
| A.平行于同一平面的两条直线平行; | B.与某一平面成等角的两条直线平行; |
| C.垂直于同一平面的两条直线平行; | D.垂直于同一直线的两条直线平行。 |
设p:y=cx是R上的单调递减函数;q:函数g(x)=lg(2cx2+2x+1)的值域为R.如果“p且q”为假命题,“p或q”为真命题,则正实数c的取值范围是( )
 C.
C. ∪[1,+∞)
∪[1,+∞) 
已知命题p:“若a>b>0,则log b”,其命题p的原命题?逆命题?否命题?逆否命题中为真命题的个数为( )
b”,其命题p的原命题?逆命题?否命题?逆否命题中为真命题的个数为( )
| A.0 | B.1 | C.2 | D.4 |
关于命题 ,使
,使 ;命题
;命题 ,都有
,都有 .有下列结论中正确的是 ( )
.有下列结论中正确的是 ( )
A.命题“ ”是真命题 ”是真命题 |
B.命题“ ”是真命题 ”是真命题 |
C.命题“ ”是真命题 ”是真命题 |
D.命题 “ “ ”是假命题 ”是假命题 |
以下四个命题:
①过一点有且仅有一个平面与已知直线垂直;
②若平面外两点到平面的距离相等,则过这两点的直线必平行于该平面;
③两条相交直线在同一平面内的射影必为相交直线;
④两个互相垂直的平面,一个平面内的任一直线必垂直于另一平面的无数条直线.
其中正确的命题是( )
| A.①和② | B.②和③ | C.③和④ | D.①和④ |
已知直线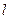 ∥平面
∥平面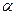 ,直线
,直线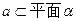 ,则直线
,则直线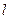 与
与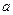 的位置关系是( )
的位置关系是( )
| A.平行 | B.异面 | C.相交 | D.平行或异面 |
下列命题中正确的是( )
| A.垂直于同一直线的两条直线平行; |
| B.若一直线垂直两条平行线中的一条,则它也垂直于另一条; |
C.若一直线相交于两平行线 中的一条,则它也相交于另一条; 中的一条,则它也相交于另一条; |
| D.一条直线至多与两条异面直线中的一条相交。 |
在下列各命题中为真命题的是( )
①若 =(x1,y1)、
=(x1,y1)、 =(x2,y2),则
=(x2,y2),则 ·
· =x1y1+x2y2
=x1y1+x2y2
②若A(x1,y1)、B(x2,y2),则| |=
|=
③若 =(x1,y1
=(x1,y1 )、
)、 =(x2,y2),则
=(x2,y2),则 ·
· =0
=0 x1x2+y1y2=0
x1x2+y1y2=0
④若 =(x1,y1)、
=(x1,y1)、 =(x2,y2),则
=(x2,y2),则 ⊥
⊥
 x1x2+y1y2=0
x1x2+y1y2=0
A.①② |
B.②③ | C.③④ | D.①④ |
.定义在实数集R上的函数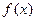 ,如果存在函数
,如果存在函数 (A,B为常数),使得
(A,B为常数),使得  对一切实数
对一切实数 都成立,那么称为
都成立,那么称为  为函
为函 数
数 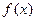 的一个承托函数,给出如下命题:
的一个承托函数,给出如下命题:
(1)定义域和值域都是R的函数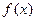 不存在承托函数;
不存在承托函数;
(2) 为函数
为函数 的一个承托函数;
的一个承托函数;
(3) 为函数
为函数 的一个承托函数;
的一个承托函数;
(4)函数 ,若函数
,若函数 的图象恰为
的图象恰为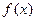 在点
在点 处的切线,则
处的切线,则 为函数
为函数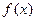 的一个承托函数。
的一个承托函数。
其中正确的命题的个数是( )
| A.0 | B.1 | C.2 | D.3 |