对于在区间 上有意义的两个函数
上有意义的两个函数 ,如果对于任意的
,如果对于任意的 ,都有
,都有 则称
则称 在区间
在区间 上是“接近的”两个函数,否则称它们在区间
上是“接近的”两个函数,否则称它们在区间 上是“非接近的”两个函数。现有两个函数
上是“非接近的”两个函数。现有两个函数 给定一个区间
给定一个区间 。
。
(1)若 在区间
在区间 有意义,求实数
有意义,求实数 的取值范围;
的取值范围;
(2)讨论 在区间
在区间 上是否是“接近的”。
上是否是“接近的”。
具有性质: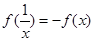 的函数,我们称为满足“倒负”变换的函数,下列函数:①
的函数,我们称为满足“倒负”变换的函数,下列函数:①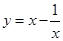 ;②
;②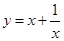 ;③
;③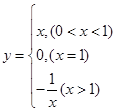 中满足“倒负”变换的函数是( )
中满足“倒负”变换的函数是( )
| A.①② | B.①③ | C.②③ | D.只有① |
已知函数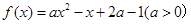
(Ⅰ)设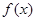 在区间
在区间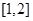 的最小值为
的最小值为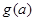 ,求
,求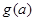 的表达式;
的表达式;
(Ⅱ)设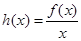 ,若函数
,若函数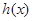 在区间
在区间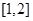 上是增函数,求实数
上是增函数,求实数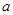 的取值范围。
的取值范围。
如果若干个函数的图象经过平移后能够重合,则称这些函数为“互为生成函数”。给出下列函数① ;②
;② ;③
;③ ;④
;④ 其中“互为生成函数”的是( )
其中“互为生成函数”的是( )
| A.①② | B.①③ | C.③④ | D.②④ |
函数 的定义域为R,且定义如下:
的定义域为R,且定义如下: (其中M是实数集R的非空真子集),在实数集R上有两个非空真子集A、B满足
(其中M是实数集R的非空真子集),在实数集R上有两个非空真子集A、B满足 ,则函数
,则函数 的值域为 ( )
的值域为 ( )
A. |
B. |
C. |
D. |
已知函数 的定义域为R,其导函数
的定义域为R,其导函数 的图像如图所示,则对于任意
的图像如图所示,则对于任意 ,
,
 (
( ),下列结论正确的是( )
),下列结论正确的是( )
① <0恒成立 ②
<0恒成立 ② ;③
;③ ;
;
④ ;⑤
;⑤ 。
。
| A.①③ | B.①③④ | C.②④ | D.②⑤ |