(本小题满分12分) 已知方程
 (
( 为实数)有两个不相等的实数根,分别求:
为实数)有两个不相等的实数根,分别求:
(Ⅰ)若方程 的根为一正一负,则求实数
的根为一正一负,则求实数 的取值范围;
的取值范围;
(Ⅱ)若方程 的两根都在
的两根都在 内,则求实数
内,则求实数 的取值范围
的取值范围
设 ,函数
,函数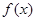 的图像与函数
的图像与函数 的图像关于点
的图像关于点 对称.
对称.
(1)求函数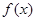 的解析式;
的解析式;
(2)若关于 的方程
的方程 有两个不同的正数解,求实数
有两个不同的正数解,求实数 的取值范围.
的取值范围.
已知函数f(x)是定义在(0,+∞)上的单调增函数,满足f(xy)=f(x)+f(y),f(3)=1
(1)求f(1)的值
(2)若满足f(x) +f(x-8)≤2 求x的取值范围
如果函数 的定义域为
的定义域为 ,对于定义域内的任意
,对于定义域内的任意 ,存在实数
,存在实数 使得
使得 成立,则称此函数具有“
成立,则称此函数具有“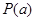 性质”.
性质”.
(1)判断函数 是否具有“
是否具有“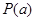 性质”,若具有“
性质”,若具有“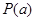 性质”求出所有
性质”求出所有 的值;若不具有“
的值;若不具有“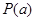 性质”,请说明理由.
性质”,请说明理由.
(2)已知 具有“
具有“ 性质”,且当
性质”,且当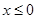 时
时 ,求
,求 在
在 上的最大值.
上的最大值.
(3)设函数 具有“
具有“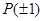 性质”,且当
性质”,且当 时,
时, .若
.若 与
与 交点个数为2013个,求
交点个数为2013个,求 的值.
的值.
函数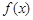 由下表定义:
由下表定义:
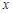 |
1 |
2 |
3 |
4 |
5 |
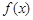 |
4 |
1 |
3 |
5 |
2 |
若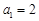 ,
,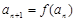 ,
,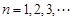 ,则
,则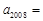 .
.
已知 是函数
是函数 的两个零点,函数
的两个零点,函数 的最小值为
的最小值为 ,记
,记
(ⅰ)试探求 之间的等量关系(不含
之间的等量关系(不含 );
);
(ⅱ)当且仅当 在什么范围内,函数
在什么范围内,函数 存在最小值?
存在最小值?
(ⅲ)若 ,试确定
,试确定 的取值范围。
的取值范围。