高中数学函数迭代试题

设A={x|}，B={y|1},下列图形表示集合A到集合B的函数图形的是（  ）

已知函数,，设.
（1）求的单调区间；
（2）若以图象上任意一点为切点的切线的斜率
恒成立，求实数的最小值.
（3）是否存在实数，使得函数的图象与的图
象恰好有四个不同的交点？若存在，求出的取值范围，若不存在，说明理由.

若函数和函数的图象恒过同一个定点，则＋的最小值为________．

设，.
（1）若恒成立，求实数的取值范围；
（2）若时，恒成立，求实数的取值范围；
（3）当时，解不等式.

关于的函数，有下列结论：
①、该函数的定义域是；            ②、该函数是奇函数；
③、该函数的最小值为；
④、当 时为增函数，当时为减函数；
其中，所有正确结论的序号是            。

若函数f(x)=,若f(a)>f(-a),则实数a的取值范围是

A．（-1，0）∪（0，1）

B．（-∞，-1）∪（1,+∞）

C．（-1，0）∪（1,+∞）

D．（-∞，-1）∪（0,1）

设为表示不超过的最大整数,则函数的定义域为 (     )

A．

B．

C．

D．

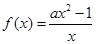若函数在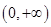上单调递增，那么实数的取值范围是（    ）

A．

B．

C．

D．

设在上是单调递增函数，当时，，且，则（   ）

A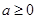．	B．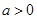
C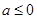．	D．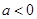

（本小题满分14分）
已知函数，，函数的图象在点处的切线平行于轴．
（1）确定与的关系；
（2）试讨论函数的单调性；
（3）证明：对任意，都有成立．

已知函数，若，则实数的取值范围是        ．

对于在区间上有意义的两个函数和，如果对于任意的，都有，则称与在区间上是接近的两个函数，否则称它们在上是非接近的两个函数。现有两个函数，，且与在都有意义.
（1）求的取值范围；
（2）讨论与在区间上是否是接近的两个函数.

已知函数，曲线在点M处的切线恰好与直线垂直。
（1）求实数的值；
（2）若函数的取值范围。

已知函数.
(1)若，函数是R上的奇函数，当时，(i)求实数与
的值；(ii)当时，求的解析式；
(2)若方程的两根中，一根属于区间，另一根属于区间，求实数的取 值范围.

下列函数中，在其定义域内既是奇函数又是减函数的是（    ）

A．

B．

C．

D．