(本小题满分14分)已知函数 有下列性质:“若
有下列性质:“若 ,使得
,使得 ”成立。
”成立。
(1)利用这个性质证明 唯一;
唯一;
(2)设A、B、C是函数 图象上三个不同的点,试判断△ABC的形状,并说明理由。
图象上三个不同的点,试判断△ABC的形状,并说明理由。
函数 的定义域为
的定义域为 ,若
,若 ,
, 且
且 时总有
时总有 ,则称
,则称 为单函数,
为单函数,
则:①函数 是单函数;②函数
是单函数;②函数 是单函数;③若
是单函数;③若 为单函数,
为单函数, ,
, 且
且 ,则
,则 ;④若函数
;④若函数 在定义域内某个区间
在定义域内某个区间 上具有单调性,则
上具有单调性,则 一定
一定
是单函数;以上命题正确的是( )
| A.①④ | B.②③ | C.①③ | D.①③④ |
设定义在D上的函数 在点
在点 处的切线方程为
处的切线方程为 ,当
,当 时,若
时,若 在D内恒成立,则称P为函数
在D内恒成立,则称P为函数 的“类对称点”,则
的“类对称点”,则 的“类对称点”的横坐标是
的“类对称点”的横坐标是
| A.1 | B. |
C.e | D. |
设是正整数,
为正有理数.
(1)求函数的最小值;
(2)证明:;
(3)设,记
为不小于
的最小整数,例如
.令
的值.
(参考数据:.
定义 ,已知实数x,y满足|x|≤2,|y|≤2,
,已知实数x,y满足|x|≤2,|y|≤2,
设 则z的取值范围是 ( )
则z的取值范围是 ( )
| A.[-7,10] | B.[-6,10] | C.[-6,8] | D.[-7,8] |
设 与
与 是定义在同一区间
是定义在同一区间 上的两个函数,若函数
上的两个函数,若函数 上有两个不同的零点,则称
上有两个不同的零点,则称 和
和 在
在 上是“关联函数”,区间
上是“关联函数”,区间 称为“关联区间”。若
称为“关联区间”。若 上是“关联函数”,则m的取值范围为( )
上是“关联函数”,则m的取值范围为( )
A. |
B. |
C. |
D. |
给出下列四个结论:①函数 在其定义域内是增函数;②函数
在其定义域内是增函数;②函数 的图象关于直线
的图象关于直线 对称;③函数
对称;③函数 的最小正周期是2π;④函数
的最小正周期是2π;④函数 是偶函数.其中正确结论的序号是 .
是偶函数.其中正确结论的序号是 .
已知函数 在
在 上是减函数,在
上是减函数,在 上是增函数,函数
上是增函数,函数 在
在 上有三个零点,且1是其中一个零点.
上有三个零点,且1是其中一个零点.
(1)求 的值;
的值;
(2)求 的取值范围;
的取值范围;
(3)试探究直线 与函数
与函数 的图像交点个数的情况,并说明理由.
的图像交点个数的情况,并说明理由.
幂指函数 在求导时,可运用对数法:在函数解析式两边求对数得
在求导时,可运用对数法:在函数解析式两边求对数得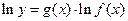 ,两边同时求导得
,两边同时求导得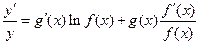 ,于是
,于是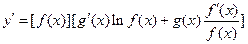 .运用此方法可以探求
.运用此方法可以探求 的一个单调递增区间是( )
的一个单调递增区间是( )
A.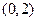 |
B.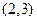 |
C.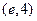 |
D.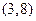 |
将边长为2的等边 沿
沿 轴正方向滚动,某时刻
轴正方向滚动,某时刻 与坐标原点重合(如图),设顶点
与坐标原点重合(如图),设顶点 的轨迹方程是
的轨迹方程是 ,关于函数
,关于函数 的有下列说法:
的有下列说法:
① 的值域为
的值域为 ;
;
② 是周期函数;
是周期函数;
③ ;
;
④ ,其中正确的个数是( )
,其中正确的个数是( ) 
| A.0 | B.1 | C.2 | D.3 |
如果函数 的定义域为R,对于定义域内的任意
的定义域为R,对于定义域内的任意 ,存在实数
,存在实数 使得
使得 成立,则称此函数具有“
成立,则称此函数具有“ 性质”。
性质”。
(1)判断函数 是否具有“
是否具有“ 性质”,若具有“
性质”,若具有“ 性质”,求出所有
性质”,求出所有 的值;若不具有“
的值;若不具有“ 性质”,说明理由;
性质”,说明理由;
(2)已知 具有“
具有“ 性质”,且当
性质”,且当 时
时 ,求
,求 在
在 上有最大值;
上有最大值;
(3)设函数 具有“
具有“ 性质”,且当
性质”,且当 时,
时, .若
.若 与
与 交点个数为2013,求
交点个数为2013,求 的值.
的值.
已知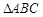 的三内角分别为
的三内角分别为 ,向量
,向量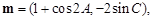
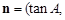
 ,记函数
,记函数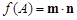 .
.
(1)若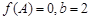 ,求
,求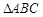 的面积;
的面积;
(2)若关于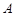 的方程
的方程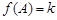 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围.
的取值范围.