有一个公益广告说:“若不注意节约用水,那么若干年后,最有一滴水只能是我们的眼泪。”我国是水资源匮乏的国家。为鼓励节约用水,某市打算出台一项水费政策措施,规定:每一季度每人用水量不超过5吨时,每吨水费收基本价1.3元;若超过5吨而不超过6吨时,超过部分的水费加收200%;若超过6吨而不超过7吨时,超过部分的水费加收400%。设某人本季度实际用水量为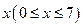 吨,应交水费为f(x),
吨,应交水费为f(x),
(1)求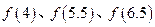 的值;
的值;
(2)试求出函数f(x)的解析式。
已知函数 有如下性质:如果常数
有如下性质:如果常数 ,那么该函数在
,那么该函数在 上是减函数,在
上是减函数,在 上是增函数。
上是增函数。
(1)如果函数 在
在 上是减函数,在
上是减函数,在 上是增函数,求
上是增函数,求 的值。
的值。
(2)设常数 ,求函数
,求函数 的最大值和最小值;
的最大值和最小值;
.(本小题满分14分)
设 实数
实数 、
、 同时满足条件:
同时满足条件: ,且
,且 ,
,
(1)求函数 的解析式和定义域;
的解析式和定义域;
(2)判断函数 的奇偶性;
的奇偶性;
(3)若方程 恰有两个不同的实数根,求
恰有两个不同的实数根,求 的取值范围
的取值范围
(本小题满分12分)
设p:实数x满足
(1)若 为真,求实数x的取值范围;
为真,求实数x的取值范围;
(2)若p是q的充分不必要条件,求实数a的取值范围.
某公园准备建一个摩天轮,摩天轮的外围是一个周长为 米的圆.在这个圆上安装座位,且每个座位和圆心处的支点都有一根直的钢管相连.经预算,摩天轮上的每个座位与支点相连的钢管的费用为
米的圆.在这个圆上安装座位,且每个座位和圆心处的支点都有一根直的钢管相连.经预算,摩天轮上的每个座位与支点相连的钢管的费用为 元/根,且当两相邻的座位之间的圆弧长为
元/根,且当两相邻的座位之间的圆弧长为 米时,相邻两座位之间的钢管和其中一个座位的总费用为
米时,相邻两座位之间的钢管和其中一个座位的总费用为 元,假设座位等距离分布,且至少有四个座位,
元,假设座位等距离分布,且至少有四个座位,
所有座位都视为点,且不考虑其他因素,记摩天轮的总造价为 元.
元.
(Ⅰ)试写出 关于
关于 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(Ⅱ)当 米时,试确定座位的个数,使得总造价最低。
米时,试确定座位的个数,使得总造价最低。
(本小题满分12分)(注意:在试题卷上作答无效)
已知函数 .
.
(Ⅰ)若曲线 在
在 和
和 处的切线互相平行,求
处的切线互相平行,求 的值;
的值;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)设 ,若对任意
,若对任意 ,均存在
,均存在 ,使得
,使得 ,求
,求 的取值范围.
的取值范围.