已知函数 ,
,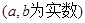 ,
,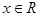 .
.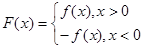
(1)若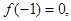 且函数
且函数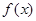 的值域为
的值域为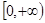 ,求
,求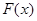 的表达式;
的表达式;
(2)在(1)的条件下,当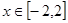 时,
时,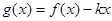 是单调函数,求实数
是单调函数,求实数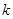 的取值范围;
的取值范围;
(3)设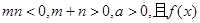 为偶函数,判断
为偶函数,判断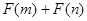 能否大于零?
能否大于零?
已知集合 是满足下列性质函数的
是满足下列性质函数的 的全体,在定义域
的全体,在定义域 内存在
内存在 ,使得
,使得 成立。(1)函数
成立。(1)函数 ,
, 是否属于集合
是否属于集合 ?分别说明理由。(2)若函数
?分别说明理由。(2)若函数 属于集合
属于集合 ,求实数
,求实数 的取值范围。
的取值范围。
已知函数 与
与
(1)设直线 分别相交于点
分别相交于点 ,且曲线
,且曲线 和
和 在点
在点 处的切线平行,求实数
处的切线平行,求实数 的值;
的值;
(2) 为
为 的导函数,若对于任意的
的导函数,若对于任意的 ,
, 恒成立,求实数
恒成立,求实数 的最大值;
的最大值;
(3)在(2)的条件下且当 取
取 最大值的
最大值的 倍时,当
倍时,当 时,若函数
时,若函数 的最小值恰为
的最小值恰为 的最小值,求实数
的最小值,求实数 的值
的值
(小题满分14分)已知定义域为R的函数 是奇函数.
是奇函数.
(1)求 的值;
的值;
(2)若对任意的 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
已知定义在R上的函数f(x) 同时满足:① (
( R,a为常数);②
R,a为常数);② ;③当
;③当 时,
时, ≤2。
≤2。
求:(Ⅰ)函数 的解析式;(Ⅱ)常数a的取值范围。
的解析式;(Ⅱ)常数a的取值范围。
已知函数
(1)当
时,求不等式
的解集;
(2)若
的解集包含
,求
的取值范围.
若函数 在定义域内存在区间
在定义域内存在区间 ,满足
,满足 在
在 上的值域为
上的值域为 ,则称这样的函数
,则称这样的函数 为“优美函数”.
为“优美函数”.
(Ⅰ)判断函数 是否为“优美函数”?若是,求出
是否为“优美函数”?若是,求出 ;若不是,说明理由;
;若不是,说明理由;
(Ⅱ)若函数 为“优美函数”,求实数
为“优美函数”,求实数 的取值范围.
的取值范围.