 ,则称
,则称 为
为 与
与
在 上的一个“分界函数”.如
上的一个“分界函数”.如 ,则称
,则称 一个“分界函数”。
一个“分界函数”。
(1)求证: 是
是 和
和 在
在 上的一个“分界函数”;
上的一个“分界函数”;
(2)若 和
和 在
在 上一定存在一个“分界函数”,试确定实数
上一定存在一个“分界函数”,试确定实数 的取值范围.
的取值范围.
第一小题3分,第二小题5分,第三小题6分.
(1)已知函数 是奇函数,
是奇函数, 为常数,求实数
为常数,求实数 的值;
的值;
(2)若 ,且
,且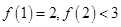 ,求
,求 的解析式;
的解析式;
(3)对于(2)中的 ,若
,若 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分13分)对于定义域为D的函数 ,若同时满足下列条件:①
,若同时满足下列条件:① 在D内单调递增或单调递减;②存在区间[
在D内单调递增或单调递减;②存在区间[ ]
] ,使
,使 在[
在[ ]上的值域为[
]上的值域为[ ];那么把
];那么把 (
( )叫闭函数。
)叫闭函数。
(1)求闭函数 符合条件②的区间[
符合条件②的区间[ ];
];
(2)判断函数 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)判断函数 是否为闭函数?若是闭函数,求实数
是否为闭函数?若是闭函数,求实数 的取值范围。
的取值范围。
给定函数 和常数
和常数 ,若
,若 恒成立,则称
恒成立,则称 为函数
为函数 的一个“好数对”;若
的一个“好数对”;若 恒成立,则称
恒成立,则称 为函数
为函数 的一个“类好数对”.已知函数
的一个“类好数对”.已知函数 的定义域为
的定义域为 .
.
(Ⅰ)若 是函数
是函数 的一个“好数对”,且
的一个“好数对”,且 ,求
,求 ;
;
(Ⅱ)若 是函数
是函数 的一个“好数对”,且当
的一个“好数对”,且当 时,
时, ,求证:
,求证:
函数 在区间
在区间 上无零点;
上无零点;
(Ⅲ)若 是函数
是函数 的一个“类好数对”,
的一个“类好数对”, ,且函数
,且函数 单调递增,比较
单调递增,比较 与
与 的大小,并说明理由.
的大小,并说明理由.
已知定理:“若 为常数,
为常数, 满足
满足 ,则函数
,则函数 的图象关于点
的图象关于点 中心对称”.设函数
中心对称”.设函数 ,定义域为A.
,定义域为A.
(1)试证明 的图象关于点
的图象关于点 成中心对称;
成中心对称;
(2)当 时,求证:
时,求证: ;
;
(3)对于给定的 ,设计构造过程:
,设计构造过程:
 ,…,
,…, .如果
.如果 ,构造过程将继续下去;如果
,构造过程将继续下去;如果 ,构造过程将停止.若对任意
,构造过程将停止.若对任意 ,构造过程可以无限进行下去,求a的值.
,构造过程可以无限进行下去,求a的值.
(本小题满分12分)定义在 上的函数
上的函数 ,如果满足:对任意
,如果满足:对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 是
是 上的有界函数,其中
上的有界函数,其中 称为函数
称为函数 的上界.已知函数
的上界.已知函数 ,
,
(1)当 时,求函数
时,求函数 在
在 上的值域,并判断函数
上的值域,并判断函数 在
在 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数 在
在 上是以4为上界的有界函数,求实数
上是以4为上界的有界函数,求实数 的取值范围.
的取值范围.
(本小题满分14分)若在定义域内存在实数 ,使得
,使得 成立,则称函数有“飘移点”
成立,则称函数有“飘移点” .
.
(1)函数 是否有“飘移点”?请说明理由;
是否有“飘移点”?请说明理由;
(2)证明函数 在
在 上有“飘移点”;
上有“飘移点”;
(3)若函数 在
在 上有“飘移点”,求实数
上有“飘移点”,求实数 的取值范围.
的取值范围.
(本小题满分14分)已知函数 ,
, ,设曲线
,设曲线 在点
在点 处的切线方程为
处的切线方程为 . 如果对任意的
. 如果对任意的 ,均有:
,均有:
①当 时,
时, ;
;
②当 时,
时, ;
;
③当 时,
时, ,
,
则称 为函数
为函数 的一个“ʃ-点”.
的一个“ʃ-点”.
(1)判断 是否是下列函数的“ʃ-点”:
是否是下列函数的“ʃ-点”:
① ; ②
; ② .(只需写出结论)
.(只需写出结论)
(2)设函数 .
.
(ⅰ)若 ,证明:
,证明: 是函数
是函数 的一个“ʃ-点”;
的一个“ʃ-点”;
(ⅱ)若函数 存在“ʃ-点”,直接写出
存在“ʃ-点”,直接写出 的取值范围.
的取值范围.
已知函数
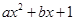 ,(1) 若
,(1) 若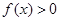 的解集是
的解集是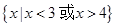 ,求实数
,求实数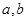 的值;(2) 若
的值;(2) 若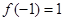 且
且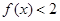 恒成立,求实数
恒成立,求实数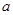 的取值范围.
的取值范围.
设
,已知函数
.
(Ⅰ)当
时,讨论函数
的单调性;
(Ⅱ)当
时,称
为
关于
的加权平均数.
(1)判断
是否成等比数列,并证明
;
(2)
的几何平均数记为
.称
为
的调和平均数,记为
.若
,求
的取值范围.
设是正整数,
为正有理数.
(1)求函数的最小值;
(2)证明:;
(3)设,记
为不小于
的最小整数,例如
.令
的值.
(参考数据:.