设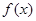 与
与 是定义在同一区间
是定义在同一区间 上的两个函数,若函数
上的两个函数,若函数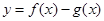 在
在 上有两个不同零点,则称
上有两个不同零点,则称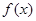 与
与 在
在 上是“关联函数”,区间
上是“关联函数”,区间 称为“关联区间”,若
称为“关联区间”,若 和
和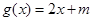 在
在 上是“关联函数”,则
上是“关联函数”,则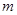 的范围为( )
的范围为( )
A. |
B.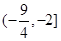 |
C. |
D.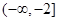 |
若函数f(x) (x∈R)是奇函数,函数g(x) (x∈R)是偶函数,则
| A.函数f[g(x)]是奇函数 | B.函数g[f(x)]是奇函数 |
| C.函数f(x) g(x)是奇函数 | D.函数f(x)+g(x)是奇函数 |
函数 的定义域是( )
的定义域是( )
A.(- ,-1) ,-1) |
B.(1,+ ) ) |
C.(-1,1)∪(1,+ ) ) |
D.(- ,+ ,+ ) ) |
定义域为R的函数 ,若对任意两个不相等的实数
,若对任意两个不相等的实数 ,都有
,都有 ,则称函数为“H函数”,现给出如下函数:
,则称函数为“H函数”,现给出如下函数:
① ②
② ③
③ ④
④
其中为“H函数”的有( )
| A.①② | B.③④ | C.②③ | D.①②③ |
若一系列函数的解析式相同,值域相同,但定义域不同,则称这些函数为“孪生函数”,那么函数解析式为y=2x2-1,值域为{1,7}的“孪生函数”共有( )
| A.10个 | B.9个 | C.8个 | D.4个 |
《莱因德纸草书》(Rh1nd Papyrus)是世界上最古老的数学著作之一,书中有这样的一道题目:把 个面包分给
个面包分给 个人,使每人所得成等差数列,且使较大的三份之和的
个人,使每人所得成等差数列,且使较大的三份之和的 是较小的两份之和,则最小
是较小的两份之和,则最小 份为
份为
A. |
B. |
C. |
D. |