设函数 的定义域为R,若存在常数M>0,使
的定义域为R,若存在常数M>0,使 对 一切实数x均成 立,则称
对 一切实数x均成 立,则称 为“倍约束函数”,现给出下列函数:①
为“倍约束函数”,现给出下列函数:① :②
:② :③
:③ ;④
;④ ⑤
⑤ 是定义在实数集R上的奇函数,且
是定义在实数集R上的奇函数,且
对一切 均有
均有 ,其中是“倍约束函数”的有( )
,其中是“倍约束函数”的有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
设 表示不超过
表示不超过 的最大整数,如
的最大整数,如 ,
, .给出下列命题:
.给出下列命题:
①对任意实数 ,都有
,都有 ;
;
②对任意实数 ,y,都有
,y,都有 ;
;
③ ;
;
④若函数 ,当
,当 时,令
时,令 的值域为A,记集合A的元素个数为
的值域为A,记集合A的元素个数为 ,则
,则 的最小值为
的最小值为 .
.
其中所有真命题的序号是_________________.
福建理)设 是
是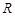 的两个非空子集,如果存在一个从
的两个非空子集,如果存在一个从 到
到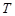 的函数
的函数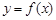 满足:
满足:
 ;
; 对任意
对任意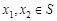 ,当
,当 时,恒有
时,恒有 ,那么称这两个集合“保序同构”,以下集合对不是“保序同构”的是( )
,那么称这两个集合“保序同构”,以下集合对不是“保序同构”的是( )
A.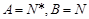 |
B.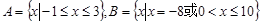 |
C. |
D.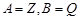 |
定义:对于函数 ,若存在非零常数
,若存在非零常数 ,使函数
,使函数 对于定义域内的任意实数
对于定义域内的任意实数 ,都有
,都有 ,则称函数
,则称函数 是广义周期函数,其中称
是广义周期函数,其中称 为函数
为函数 的广义周期,
的广义周期, 称为周距.
称为周距.
(1)证明函数 是以2为广义周期的广义周期函数,并求出它的相应周距
是以2为广义周期的广义周期函数,并求出它的相应周距 的值;
的值;
(2)试求一个函数 ,使
,使 (
( 为常数,
为常数, )为广义周期函数,并求出它的一个广义周期
)为广义周期函数,并求出它的一个广义周期 和周距
和周距 ;
;
(3)设函数 是周期
是周期 的周期函数,当函数
的周期函数,当函数 在
在 上的值域为
上的值域为 时,求
时,求 在
在 上的最大值和最小值.
上的最大值和最小值.
对于两个图形 ,我们将图形
,我们将图形 上的任意一点与图形
上的任意一点与图形 上的任意一点间的距离中的最小值,叫做图形
上的任意一点间的距离中的最小值,叫做图形 与图形
与图形 的距离.若两个函数图像的距离小于1,陈这两个函数互为“可及函数”.给出下列几对函数,其中互为“可及函数”的是_________.(写出所有正确命题的编号).
的距离.若两个函数图像的距离小于1,陈这两个函数互为“可及函数”.给出下列几对函数,其中互为“可及函数”的是_________.(写出所有正确命题的编号).
① ;
;
② ,
, ;
;
③ ,
, ;
;
④ ,
, ;
;
⑤ ,
, .
.
对于函数 ,若存在区间
,若存在区间 ,使得
,使得 ,则称函数
,则称函数 为“可等域函数”,区间
为“可等域函数”,区间 为函数
为函数 的一个“可等域区间”.给出下列4个函数:
的一个“可等域区间”.给出下列4个函数:
① ;②
;② ; ③
; ③ ; ④
; ④ .
.
其中存在唯一“可等域区间”的“可等域函数”为( )
| A.①②③ | B.②③ | C.①③ | D.②③④ |
若直角坐标平面内的亮点P,Q满足条件: P,Q都在函数y=f(x)的图像上, P,Q关于原点对称,则称点对[P,Q]是函数y=f(x)的一对“友好点对”(点对[P,Q]与[Q,P]看作同一对“友好点对”)。
已知函数 ,则此函数的“友好点对”有( )
,则此函数的“友好点对”有( )
| A.0对 | B.1对 | C.2对 | D.3对 |
已知函数 ,满足
,满足 .
.
(1)求常数c的值;
(2)解关于 的不等式
的不等式 .
.
在自然界中,存在着大量的周期函数,比如声波,若两个声波随时间的变化规律分别为: ,则这两个声波合成后即
,则这两个声波合成后即 的振幅为( )
的振幅为( )
| A.3 | B. |
C. |
D. |
对于函数 ,若
,若 为某一三角形的三边长,则称
为某一三角形的三边长,则称 为“可构造三角形函数”.已知函数
为“可构造三角形函数”.已知函数 是“可构造三角形函数”,则实数t的取值范围是( )
是“可构造三角形函数”,则实数t的取值范围是( )
A. |
B. |
C. |
D. |
若直角坐标平面内的两点P、Q满足①P、Q都在函数y=f(x)的图像上;②P、Q关于原点对称,则称点对[P,Q]是函数y=f(x)的一对“友好点对”(注:点对[P,Q]与[Q,P]看作同一对“友好点对”).
已知函数f(x)= 则此函数的“友好点对”有( )
则此函数的“友好点对”有( )
| A.0对 | B.1对 |
| C.2对 | D.3对 |
已知函数 (
( ).
).
(1)若 ,求函数
,求函数 的极值;
的极值;
(2)若 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知函数 .
.
(1)求函数 的单调区间;
的单调区间;
(2)若 ,求函数
,求函数 的值域.
的值域.
已知函数 .
.
(1)解关于 的不等式
的不等式 ;
;
(2)若 在区间
在区间 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
已知函数 (a为常数)在x=1处的切线的斜率为1.
(a为常数)在x=1处的切线的斜率为1.
(1)求实数a的值,并求函数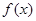 的单调区间,
的单调区间,
(2)若不等式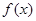 ≥k在区间
≥k在区间 上恒成立,其中e为自然对数的底数,求实数k的取值范围.
上恒成立,其中e为自然对数的底数,求实数k的取值范围.