高中数学函数迭代试题

已知函数
(1)若=,求的值
(2)

已知是一次函数，，，则的解析式为             

下列命题：①若定义D内任意实数x都有f(x+1)=f(x-1)，则y=f(x)是周期函数；
②在定义域内是增函数；  ③函数图象关于原点对称；
④既是奇函数又是偶函数的函数一定是="0" ;   
⑤函数f(x)若在定义D内的任意实数x都有f(x＋2)= f(2－x)，则f(x)图象关于直线x＝2对称；其中正确命题是             。

（本小题满分14分）设为实数，函数，
（1）当时，讨论的奇偶性；
（2）当时，求的最大值.

已知，，，则有（   ）

A．

B．

C．

D．

若是R上的减函数, 且的图象经过点(0, 4)和点(3, －2), 则当不等式 |f(x+t)－1|<3的解集为(－1, 2 ) 时, 的值为： （   ）   
 

A．0

B．－1

C．1

D．2

已知偶函数在区间上单调递增，则满足的的取值范围是

A．

B．

C．

D．

．设函数，表示不超过的最大整数，则函数
的值域为

A．

B．

C．

D．

已知函数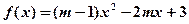是偶函数，则在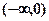上此函数  

A．是增函数

B．不是单调函数

C．是减函数

D．不能确定

．对于定义域为[0，1]的函数f(x)，如果同时满足以下三条：①对任意的x∈[0,1] ，总有；②f(1)=1；③若都有成立，则称函数f(x)为理想函数。
（1）若函数f(x)为理想函数，求f(0)的值；
（2）判断函数是否为理想函数，并予以证明。

设函数在内有定义，对于给定的正数K，定义函数       取函数。当=时，函数的单调递增区间为(      )   

A．

B．

C．

D．

定义在上的函数是奇函数，且，，则 （  ）    

A．8

B．10

C．12

D．14

已知是上的奇函数，
,则数列的通项公式为                      （     ）

A．

B．

C．

D．

，函数的单调递减区间是             .

若关于的方程在上有解，则的取值范围是

A．

B．

C．

D．