已知函数 (
( 为常数).
为常数).
(1)当 时,求
时,求 的单调递减区间;
的单调递减区间;
(2)若 ,且对任意的
,且对任意的 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知函数 ,函数
,函数
 .
.
(1)判断函数 的奇偶性;
的奇偶性;
(2)若当 时,
时, 恒成立,求实数
恒成立,求实数 的最大值.
的最大值.
给出下列函数① ②
② ③
③ ④
④ ,其中是奇函数的是( )
,其中是奇函数的是( )
| A.①② | B.①④ | C.②④ | D.③④ |
若函数 对任意的
对任意的 都有
都有 ,且
,且 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
对于函数 与
与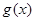 和区间D,如果存在
和区间D,如果存在 ,使
,使 ,则称
,则称 是函数
是函数 与
与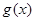 在区间D上的“友好点”.现给出两个函数
在区间D上的“友好点”.现给出两个函数
① ,
, ②
②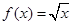 ,
,
③ ,
, ④
④ ,
,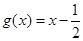
其中在区间 上存在“友好点”的有( )
上存在“友好点”的有( )
| A.①② | B.②③ | C.③④ | D.①④ |
已知函数 ,(
,( ,
, .若
.若 ,且函数
,且函数 的图像关于点
的图像关于点 对称,并在
对称,并在 处取得最小值,则正实数
处取得最小值,则正实数 的值构成的集合是 .
的值构成的集合是 .
若在曲线 上两个不同点处的切线重合,则称这条切线为曲线
上两个不同点处的切线重合,则称这条切线为曲线 或
或 的“自公切线”。
的“自公切线”。
下列方程:
① ;
;
② ;
;
③ ;
;
④
对应的曲线中存在“自公切线”的有( )
| A.①③ | B.①④ | C.②③ | D.②④ |
已知函数f(x)= -2alnx(a>0)
-2alnx(a>0)
(I)求函数f(x)的单调区间和最小值.
(II)若方程f(x)=2ax有唯一解,求实数a的值.
设F(x)=3a +2bx+c,若a+b+c=0,且F(0)>0,F(1)>0.
+2bx+c,若a+b+c=0,且F(0)>0,F(1)>0.
求证:a>0,且—2<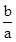 <—1.
<—1.
定义在区间 上的奇函数
上的奇函数 为增函数,偶函数
为增函数,偶函数 在
在 上图象与
上图象与 的图象重合.设
的图象重合.设 ,给出下列不等式,其中成立的是( )
,给出下列不等式,其中成立的是( )
①
②
③
④
| A.①④ | B.②③ | C.①③ | D.②④ |