函数 在区间
在区间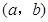 内函数的导数为正,且
内函数的导数为正,且 ≤0,则函数
≤0,则函数 在
在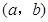 内有
内有
A. <0 <0 |
B. >0 >0 |
C. = 0 = 0 |
D.无法确定 |
设f(x)是定义在R上的奇函数,且f(2)=0,当x>0时,有 恒成立,则不等式
恒成立,则不等式 的解集是( )
的解集是( )
| A.(-2,0)∪(2,+∞) | B.(-2,0)∪(0,2) |
| C.(-∞,-2)∪(2,+∞) | D.(-∞,-2)∪(0,2) |
对于定义在R上的函数 ,有下述命题:
,有下述命题:
①若 是奇函数,则
是奇函数,则 的图象关于点A(1,0)对称
的图象关于点A(1,0)对称
②若函数 的图象关于直线
的图象关于直线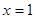 对称,则
对称,则 为偶函数
为偶函数
③若对 ,有
,有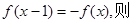 2是
2是 的一个周期为
的一个周期为
④函数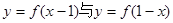 的图象关于直线
的图象关于直线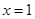 对称.
对称.
其中正确的命题是___ .(写出所有正确命题的序号)
已知定义在R上的函数f(x) 同时满足:① (
( R,a为常数);②
R,a为常数);② ;③当
;③当 时,
时, ≤2。
≤2。
求:(Ⅰ)函数 的解析式;(Ⅱ)常数a的取值范围。
的解析式;(Ⅱ)常数a的取值范围。
函数 的定义域为
的定义域为 ,若存在非零实数
,若存在非零实数 使得对于任意
使得对于任意 ,有
,有 ,且
,且 ,则称
,则称 为
为 上的
上的 高调函数。如果定义域为
高调函数。如果定义域为 的函数
的函数 是奇函数,当
是奇函数,当 时,
时, ,且
,且 为
为 上的4高调函数,那么实数
上的4高调函数,那么实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
定义在 上的偶函数
上的偶函数 在[—1,0]上是增函数,给出下列关于
在[—1,0]上是增函数,给出下列关于 的判断:
的判断:
① 是周期函数;
是周期函数;
② 关于直线
关于直线 对称;
对称;
③ 是[0,1]上是增函数;
是[0,1]上是增函数;
④ 在[1,2]上是减函数;
在[1,2]上是减函数;
⑤ .
.
其中正确的序号是 . (把你认为正确的序号都写上)