设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为 和
和 组成数对(
组成数对( ,并构成函数
,并构成函数
(Ⅰ)写出所有可能的数对( ,并计算
,并计算 ,且
,且 的概率;
的概率;
(Ⅱ)求函数 在区间[
在区间[ 上是增函数的概率.
上是增函数的概率.
(本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.
已知函数 =
= .
.
(1)判断函数 的奇偶性,并证明;
的奇偶性,并证明;
(2)求 的反函数
的反函数 ,并求使得函数
,并求使得函数 有零点的实数
有零点的实数 的取值范围.
的取值范围.
若函数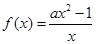 在
在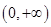 上单调递增,那么实数
上单调递增,那么实数 的取值范围是( )
的取值范围是( )
A.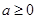 |
B.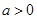 |
C.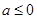 |
D.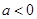 |
函数 ,其中
,其中 ,若动直线
,若动直线 与函数
与函数 的图像有三个不同的交点,则实数
的图像有三个不同的交点,则实数 的取值范围是______________.
的取值范围是______________.
如果函数 的定义域为
的定义域为 ,对于定义域内的任意
,对于定义域内的任意 ,存在实数
,存在实数 使得
使得 成立,则称此函数具有“
成立,则称此函数具有“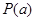 性质”.
性质”.
(1)判断函数 是否具有“
是否具有“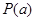 性质”,若具有“
性质”,若具有“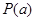 性质”求出所有
性质”求出所有 的值;若不具有“
的值;若不具有“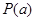 性质”,请说明理由.
性质”,请说明理由.
(2)已知 具有“
具有“ 性质”,且当
性质”,且当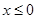 时
时 ,求
,求 在
在 上的最大值.
上的最大值.
(3)设函数 具有“
具有“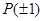 性质”,且当
性质”,且当 时,
时, .若
.若 与
与 交点个数为2013个,求
交点个数为2013个,求 的值.
的值.
定义域是一切实数的函数 ,其图像是连续不断的,且存在常数
,其图像是连续不断的,且存在常数 (
( )使得
)使得  对任意实数
对任意实数 都成立,则称
都成立,则称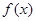 是一个“
是一个“ —伴随函数”.有下列关于“
—伴随函数”.有下列关于“ —伴随函数”的结论:
—伴随函数”的结论:
① 是常数函数中唯一一个“
是常数函数中唯一一个“ —伴随函数”;
—伴随函数”;
②“ —伴随函数”至少有一个零点;
—伴随函数”至少有一个零点;
③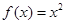 是一个“
是一个“ —伴随函数”;
—伴随函数”;
其中正确结论的个数是 ( )
| A.1个; | B.2个; | C.3个; | D.0个; |
对于函数f (x)和g(x),其定义域为[a, b],若对任意的x∈[a, b]总有|1- |≤
|≤ ,则称f (x)可被g(x)置换,那么下列给出的函数中能置换f (x)=
,则称f (x)可被g(x)置换,那么下列给出的函数中能置换f (x)= x∈[4,16]的是 ( )
x∈[4,16]的是 ( )
| A.g(x)=2x+6 x∈[4,16] | B.g(x)=x2+9 x∈[4,16] |
C.g(x)=  (x+8) x∈[4,16] (x+8) x∈[4,16] |
D.g(x)= (x+6) x∈[4,16] (x+6) x∈[4,16] |
下列说法正确的是
A.函数 在其定义域上是减函数 在其定义域上是减函数 |
| B.两个三角形全等是这两个三角形面积相等的必要条件 |
C.命题“ R, R, ”的否定是“ ”的否定是“  R, R, ” ” |
D.给定命题 、 、 ,若 ,若 是真命题,则 是真命题,则 是假命题 是假命题 |
已知函数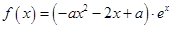 ,
,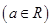
(1)当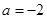 时,求函数
时,求函数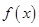 的极值;
的极值;
(2) 若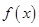 在[-1,1]上单调递减,求实数
在[-1,1]上单调递减,求实数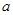 的取值范围.
的取值范围.