(本小题满分14分)已知函数 。
。
(Ⅰ)若函数 在定义域内为增函数,求实数
在定义域内为增函数,求实数 的取值范围;
的取值范围;
(Ⅱ)设 ,若函数
,若函数 存在两个零点
存在两个零点 ,且满足
,且满足 ,问:函数
,问:函数 在
在 处的切线能否平行于
处的切线能否平行于 轴?若能,求出该切线方程;若不能,请说明理由。
轴?若能,求出该切线方程;若不能,请说明理由。
(本小题满分12分)
设函数 ,其中
,其中 表示不超过
表示不超过 的最大整数,如
的最大整数,如 .
.
(1)求 的值;
的值;
(2)若在区间 上存在x,使得
上存在x,使得 成立,求实数k的取值范围;
成立,求实数k的取值范围;
(3)求函数 的值域.
的值域.
若函数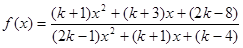 的定义域用D表示,则使
的定义域用D表示,则使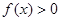 对
对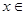 D均成立的实数
D均成立的实数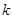 的范围是___
的范围是___
函数y = 1n|x-1|的图像与函数y="-2" cos  x(-2≤x≤4)的图像所有交点的横坐标之和等于
x(-2≤x≤4)的图像所有交点的横坐标之和等于
| A.8 | B.6 | C.4 | D.2 |
已知函数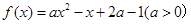
(Ⅰ)设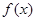 在区间
在区间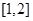 的最小值为
的最小值为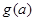 ,求
,求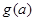 的表达式;
的表达式;
(Ⅱ)设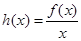 ,若函数
,若函数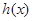 在区间
在区间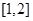 上是增函数,求实数
上是增函数,求实数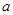 的取值范围。
的取值范围。
(本小题满分16分)已知函数 (
( 为常数)是实数集
为常数)是实数集 上的奇函数,函数
上的奇函数,函数 是区间
是区间 上的减函数。
上的减函数。
(1)求 在
在 上的最大值;
上的最大值;
(2)若 对
对 及
及 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(3)讨论关于 的方程
的方程 的根的个数。
的根的个数。
定义函数 ,若存在常数C,对任意的
,若存在常数C,对任意的 ,存在唯一的
,存在唯一的 ,使得
,使得 ,则称函数
,则称函数 在D上的几何平均数为C.已知
在D上的几何平均数为C.已知 ,则函数
,则函数 在
在 上的几何平均数为( )
上的几何平均数为( )
A. B.
B. C.
C. D.
D.
(本小题满分12分)
已知函数
(1)是否存在实数
 ,使得函数
,使得函数 的定义域、值域都是
的定义域、值域都是 ,若存在,则求出
,若存在,则求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
(2)若存在实数
 ,使得函数
,使得函数 的定义域为
的定义域为 时,值域为
时,值域为 (
( ),求
),求 的取值范围.
的取值范围.