(本小题满分12分)
已知函数:
 .
.
(1) 当 时①求
时①求 的单调区间;
的单调区间;
②设 ,若对任意
,若对任意 ,存在
,存在 ,使
,使 ,求实数
,求实数 取值范围.
取值范围.
(2) 当 时,恒有
时,恒有 成立,求
成立,求 的取值范围.
的取值范围.
如果若干个函数的图象经过平移后能够重合,则称这些函数为“互为生成函数”。给出下列函数① ;②
;② ;③
;③ ;④
;④ 其中“互为生成函数”的是( )
其中“互为生成函数”的是( )
| A.①② | B.①③ | C.③④ | D.②④ |
函数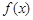 由下表定义:
由下表定义:
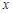 |
1 |
2 |
3 |
4 |
5 |
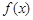 |
4 |
1 |
3 |
5 |
2 |
若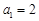 ,
,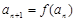 ,
,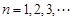 ,则
,则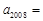 .
.
已知函数 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时,
时,
(1)求 的解析式
的解析式
(2)解关于 的不等式
的不等式
对于实数 ,符号
,符号 表示不超过
表示不超过 的最大整数,例如
的最大整数,例如 ,定义函数
,定义函数 ,则下列命题中正确的是 (填题号)
,则下列命题中正确的是 (填题号)
①函数 的最大值为1;②函数
的最大值为1;②函数 的最小值为0;
的最小值为0;
③函数 有无数个零点;④函数
有无数个零点;④函数 是增函数
是增函数
已知f (x)、g(x)都是定义在R上的函数,如果存在实数m、n使得h (x) =" m" f(x)+ng(x),那么称h (x)为f (x)、g(x)在R上生成的函数.设 ,
, ,若h (x)为f (x)、g(x)在R上生成的一个偶函数,且
,若h (x)为f (x)、g(x)在R上生成的一个偶函数,且 ,则函数h (x)="__________."
,则函数h (x)="__________."
(本小题满分12分)
设 为实数,且
为实数,且
(1)求方程 的解;
的解;
(2)若 ,
, 满足
满足 ,试写出
,试写出 与
与 的等量关系(至少写出两个);
的等量关系(至少写出两个);
(3)在(2)的基础上,证明在这一关系中存在 满足
满足 .
.
(本小题满分12分)
已知常数 ,函数
,函数
(1)求 ,
, 的值;
的值;
(2)讨论函数 在
在 上的单调性;
上的单调性;
(3)求出 在
在 上的最小值与最大值,并求出相应的自变量的取值.
上的最小值与最大值,并求出相应的自变量的取值.
(本小题满分12分)
已知函数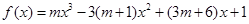 其中
其中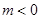
(1)、若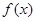 的单调增区间是(0.1),求m的值
的单调增区间是(0.1),求m的值
(2)、当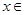
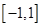 时,函数
时,函数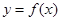 的图像上任意一点的切线斜率恒大于3m,求m的取值范围.
的图像上任意一点的切线斜率恒大于3m,求m的取值范围.