某工厂有甲、乙、丙三类产品的数量成等比数列且公比为2,现要用分层抽样的方法从中抽取140件进行质量检测,则乙类产品应抽 件
将正偶数集合{2,4,6,…}从小到大按第 组有
组有 个偶数进行分组,{2},{4,6,8} ,{10,12,14,16,18},…第一组、第二组、第三组,则2010位于第 组。( )
个偶数进行分组,{2},{4,6,8} ,{10,12,14,16,18},…第一组、第二组、第三组,则2010位于第 组。( )
| A.30 | B.31 | C.32 | D.33 |
已知 是首项为1的等比数列,
是首项为1的等比数列, 是
是 的前n项和,且
的前n项和,且 ,则数列
,则数列 的前5项和为
的前5项和为
A. 或5 或5 |
B. 或5 或5 |
C. |
D. |
设数列 的前
的前 项和为
项和为 。
。
(1)证明: 为等比数列;
为等比数列;
(2)证明:求数列 的通项公式;
的通项公式;
(3)确定 与
与 的大小关系,并加以证明。
的大小关系,并加以证明。
随着科学技术的不断发展,人类通过计算机已找到了630万位的最大质数。陈成在学习中发现由41,43,47,53,61,71,83,97组成的数列中每一个数都是质数,他根据这列数的一个通项公式,得出了数列的后几项,发现它们也是质数。于是他断言:根据这个通项公式写出的数均为质数。请你写出这个通项公式 ,从这个通项公式举出一个反例,说明陈成的说法是错误的: .
由公差 的等差数列{an}中的项组成一个新数列
的等差数列{an}中的项组成一个新数列 ,
,  ,
, ,…,则下列说法正确的是
,…,则下列说法正确的是
| A.该数列不是等差数列 | B.该数列是公差为 的等差数列 的等差数列 |
C.该数列是公差为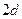 的等差数列 的等差数列 |
D.该数列是公差为 的等差数列 的等差数列 |
(本小题满分14分)
已知等差数列 的公差为
的公差为 ,且
,且 ,数列
,数列 的前
的前 项和为
项和为 ,且
,且

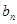


(1)求数列 ,
, 的通项公式;
的通项公式;
(2)记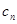 =
= 求证:数列
求证:数列 的前
的前 项和
项和  。
。