在数列{an}中,a1=2,an+1=an+ln(1+ ),则an=( )
),则an=( )
| A.2+lnn | B.2+(n-1)lnn | C.2+nlnn | D.1+n+lnn |
在数列{an}中,a1=1,anan-1=an-1+(-1)n(n≥2,n∈N*),则 的值是( )
的值是( )
A. |
B. |
C. |
D. |
在数列{ }中,已知
}中,已知

(1)求 并由此猜想数列{
并由此猜想数列{ }的通项公式
}的通项公式 的表达式;
的表达式;
(2)用数学归纳法证明你的猜想。
记等比数列 的前
的前 项积为
项积为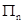 ,若
,若 ,则
,则 ( )
( )
| A.256 | B.81 | C.16 | D.1 |
已知等比数列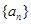 的前
的前 项积记为
项积记为 ,若
,若 ,则
,则 ( )
( )
| A.512 | B.256 | C.81 | D.16 |
如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行,依次类推,则(1)按网络运作顺序第n行第1个数字(如第2行第1个数字为2,第3行第1个数字为4,…)是__________;(2)第63行从左至右的第4个数字应是__________.
已知数列{an}满足anan+1an+2·an+3=24,且a1=1,a2=2,a3=3,则a1+a2+a3+…+a2 013=________.
设两数列{an}和{bn},an= ,bn=
,bn= ,则数列
,则数列 的前n项的和为( )
的前n项的和为( )
A. |
B. |
C. |
D. |
已知数列{an}的前n项和为Sn,把{Sn}的前n项和称为“和谐和”,用Hn来表示.对于an=3n,其“和谐和”Hn=( )
A. |
B. |
C. |
D. |
已知正数数列 中,
中, ,前
,前 项和为
项和为 ,对任意
,对任意 ,
, 、
、 、
、 成等差数列.
成等差数列.
(1)求 和
和 ;
;
(2)设 ,数列
,数列 的前
的前 项和为
项和为 ,当
,当 时,证明:
时,证明: .
.
在数列{an}中,an+1=can(c为非零常数),前n项和为Sn=3n+k,则实数k的值为( )
| A.-1 | B.0 |
| C.1 | D.2 |
如果正整数a的各位数字之和等于6,那么称a为“好数”(如:6,24,2 013等均为“好数”),将所有“好数”从小到大排成一列a1,a2,a3,…,若an=2 013,则n=( )
| A.50 | B.51 |
| C.52 | D.53 |
已知数列{an},如果数列{bn}满足b1=a1,bn=an+an-1,n≥2,n∈N*,则称数列{bn}是数列{an}的“生成数列”.
(1)若数列{an}的通项为an=n,写出数列{an}的“生成数列”{bn}的通项公式;
(2)若数列{cn}的通项为cn=2n+b(其中b是常数),试问数列{cn}的“生成数列”{qn}是否是等差数列,请说明理由;
(3)已知数列{dn}的通项为dn=2n+n,求数列{dn}的“生成数列”{pn}的前n项和Tn.