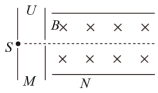
如图所示， 为粒子加速器； 为速度选择器，两平行导体板之间有方向相互垂直的匀强电场和匀强磁场，磁场的方向垂直纸面向里，磁感应强度为 。从 点释放一初速度为0、质量为 、电荷量为 的带正电粒子，经 加速后恰能以速度 沿直线（图中平行于导体板的虚线）通过 。不计重力。
（1）求粒子加速器 的加速电压 ；
（2）求速度选择器N两板间的电场强度 的大小和方向；
（3）仍从 点释放另一初速度为0、质量为 、电荷量为 的带正电粒子，离开N时粒子偏离图中虚线的距离为 ，求该粒子离开N时的动能 。
如图所示，相距3L的AB、CD两直线间的区域存在着两个大小不同、方向相反的有界匀强电场，其中PT上方的电场I的场强方向竖直向下，PT下方的电场II的场强方向竖直向上，电场I的场强大小是电场Ⅱ的场强大小的两倍，在电场左边界AB上有点Q，PQ间距离为L。从某时刻起由Q以初速度v0沿水平方向垂直射入匀强电场的带电粒子，电量为＋q、质量为m。通过PT上的某点R进入匀强电场I后从CD边上的M点水平射出，其轨迹如图，若PR两点的距离为2L。不计粒子的重力。试求：
（1）匀强电场I的电场强度E的大小和MT之间的距离；
（2）有一边长为a、由光滑弹性绝缘壁围成的正三角形容器，在其边界正中央开有一小孔S，将其置于CD右侧且紧挨CD边界，若从Q点射入的粒子经AB、CD间的电场从S孔水平射入容器中。欲使粒子在容器中与器壁多次垂直碰撞后仍能从S孔射出(粒子与绝缘壁碰撞时无机械能和电量损失)，并返回Q点，需在容器中现加上一个如图所示的匀强磁场，粒子运动的半径小于
，求磁感应强度B的大小应满足的条件以及从Q出发再返回到Q所经历的时间。
一水平传送带以4m/s的速度逆时针传送，水平部分长L=6m，其左端与一倾角为θ=300的光滑斜面平滑相连，斜面足够长，一个可视为质点的物块无初速度地放在传送带最右端，已知物块与传送带间动摩擦因数μ=0.2，g=10m/s2。求物块从放到传送带上到第一次滑回传送带最远端所用的时间。
如图所示，螺线管横截面积为S，线圈匝数为N，电阻为R1，管内有水平向右的磁场，磁感应强度为B.螺线管与足够长的平行金属导轨MN、PQ相连并固定在同一平面内，与水平面的夹角为
，两导轨间距为L。导轨电阻忽略不计。导轨处于垂直斜面向上、磁感应强度为B0的匀强磁场中。金属杆ab垂直导轨，杆与导轨接触良好，并可沿导轨无摩擦滑动。已知金属杆ab的质量为m，电阻为R2，重力加速度为g。忽略螺线管磁场对金属杆ab的影响、忽略空气阻力。
（1）螺线管内方向向右的磁场B不变，当ab杆下滑的速度为v时，求通过ab杆的电流的大小和方向；
（2）将ab杆下滑的速度为v时，螺线管内方向向右的磁场才开始变化，其变化率
（k>0）。讨论杆加速度的方向与k的取值的关系。
如图所示，在光滑水平面上停放着质量为m=2kg装有四分之一光滑圆弧形槽OPQ的物块A，圆弧形槽的半径为R=0.2m且在Q处的切线水平，物块A紧靠在与Q处等高的固定在地面上的台阶B的左端，台阶B的上表面光滑。一质量也为m=2kg的小球靠在较短的轻弹簧的左端，轻弹簧的右端固定在与台阶B连在一起的挡板上。向右移动小球压缩弹簧，当弹簧中的弹性势能达到EP=16J时，释放小球，小球冲到小车上。取g=10m/s2
求：
（1）小球刚滑到Q处时，小球对轨道Q处的压力；
（2）改变圆弧型槽的半径，小球不从P处冲出圆弧形槽，圆弧型槽半径满足的什么条件？
（3）改变圆弧型槽的半径，圆弧型槽的半径对小车的最终速度是否有影响？
粤公网安备 44130202000953号