如图所示,抗震救灾运输机在某场地通过倾角为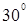 的光滑斜面卸放物资,斜面与粗糙的水平面平滑连接。现将一包装盒(可视为质点)从斜面上A点由静止释放,最终停在水平面上的C点。已知A点距水平面的高度
的光滑斜面卸放物资,斜面与粗糙的水平面平滑连接。现将一包装盒(可视为质点)从斜面上A点由静止释放,最终停在水平面上的C点。已知A点距水平面的高度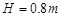 ,B点距C点的距离
,B点距C点的距离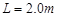 。(包装盒经过B点时速度大小不变,
。(包装盒经过B点时速度大小不变,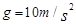 ),求:
),求: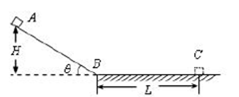
(1)包装盒在运动过程中的最大速度;
(2)包装盒与水平面间的动摩擦因数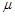 ;
;
(3)包装盒从A点释放后,经过时间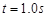 时速度的大小。
时速度的大小。
如图所示,抗震救灾运输机在某场地通过倾角为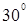 的光滑斜面卸放物资,斜面与粗糙的水平面平滑连接。现将一包装盒(可视为质点)从斜面上A点由静止释放,最终停在水平面上的C点。已知A点距水平面的高度
的光滑斜面卸放物资,斜面与粗糙的水平面平滑连接。现将一包装盒(可视为质点)从斜面上A点由静止释放,最终停在水平面上的C点。已知A点距水平面的高度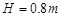 ,B点距C点的距离
,B点距C点的距离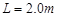 。(包装盒经过B点时速度大小不变,
。(包装盒经过B点时速度大小不变,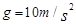 ),求:
),求:
(1)包装盒在运动过程中的最大速度;
(2)包装盒与水平面间的动摩擦因数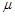 ;
;
(3)包装盒从A点释放后,经过时间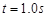 时速度的大小。
时速度的大小。