如图所示，物体A放在某一水平面上，已知物体A重60N，A与水平面之间的动摩擦因数为μ=0.3，A.B均处于静止状态，绳AC水平，绳CD与水平方向成37°角，CD绳上的拉力为15N。sin37°=0.6，cos37°=0.8．求：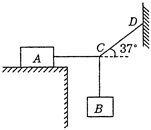
（1）物体A受到的摩擦力为多大？
（2）物体B重力为多大？
一个质量为m、带有电荷-q的小物体，可在水平轨道Ox上运动，O端有一与轨道垂直的固定墙、轨道处于匀强电场中，其场强大小为E,方向沿OX轴正方向,如图所示。小物体以初速度v0从x0点沿OX轨道运动，运动时受到大小不变的摩擦力f作用，且f＜qE；设小物体与墙碰撞时不损失机械能，且电量保持不变，求它在停止运动前所通过的总路程s。
如图所示，一个半径为R的光滑圆弧轨道APB竖直固定放置，PQ为其竖直对称轴，∠AOQ与∠BOQ都等于θ。现让一可看做质点的小球在轨道内侧运动，当其冲出A点后恰好可以从B点再进入轨道，所以此运动可以周而复始进行。已知小球质量为m，重力加速度为g，试求：
(1)小球离开轨道后的最高点距直线AB的距离；
(2)若要小球在最低点时对轨道的压力最小，θ应为多少？对应的最小压力为多少？
如图所示，在一个倾角为θ=37°(cos37°=0.8)的斜面上， O点固定一根细绳，细绳另一端连接一个质点。现将质点放到斜面上P点，由静止释放，已知OP连线水平且间距为绳长，质点滑动到细绳转过角度α=90°的位置时刚好停止。问：
(1)质点与斜面间动摩擦因数μ为多少？
(2)试描述质点放到斜面上哪些位置时可以平衡？已知最大静摩擦力与滑动摩擦力相等。
如图，在一个平面直角坐标系内，原点O处有一质点，质量为m。为使质点到达坐标为(d，d)的点P，现给质点施以大小为F的恒力，在起初的时间t1内该力方向为x轴正方向，之后的时间t2内该力变为y轴正方向，经过这两段运动质点刚好到达P点。试求：
(1)比值t1：t2；
(2)质点到达P点时的速度。
粤公网安备 44130202000953号