铁路转弯处的弯道半径,是根据地形决定的,弯道处要求外轨比内轨高,其内轨高度差五盼设计不仅与,有关,还取决于火车在弯道上行驶的速率。下表中是铁路设计人员技术手册中弯道半径r及与之相应的轨道的高度差h。
弯道半径r(m)
|
660
|
330
|
220
|
165
|
132
|
110
|
内外轨高度h(m)
|
0.05
|
0.10
|
0.15
|
0.20
|
0.25
|
0.30
|
(1)根据表中数据,试导出h与r关系的表达式,并求出当r=400m时,h的设计值。
(2)铁路建成后,火车通过弯道时,为保证绝对安全,要求内外轨道均不向车轮施加侧面压力,又已知我国铁路内外轨的距离设计值为L=1.435m,结合表中数据,求出我国火车的转弯速率v(路轨倾角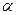 很小时,tg
很小时,tg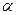 ≈sin
≈sin 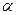 )。
)。
(3)随着人们的生活节奏加快,对交通运输的快捷提出了更高的要求,为了提高运输能力,国家对铁路不断进行提速改造,这就要求铁路转弯速率也需提高,请根据上述原理和上表分析,提速时应采取怎样的有效措施?(g取9.8m/s2)