如图所示，在倾角为37°的固定斜面上静置一个质量为5 kg的物体，物体与斜面间的动摩擦因数为0.8.求：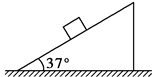
(1)物体所受的摩擦力；(sin 37°＝0.6，cos 37°＝0.8)
(2)若用原长为10 cm，劲度系数为3.1×103 N/m的弹簧沿斜面向上拉物体，使之向上匀速运动，则弹簧的最终长度是多少？(取g＝10 m/s2)
如图所示．电动机带动滚轮作逆叫针匀速转动，在滚轮的摩擦力作用下，将一金属板从斜面底端A送往上部，已知斜面光滑且足够长．倾角
=
。．滚轮与金属板的切点B到斜面底端A的距离为L=6．5m，当金属板的下端运动到切点B处时．立即提起滚轮使它与板脱离接触．已知板之后返回斜面底部与挡板相撞后立即静止．此时放下滚轮再次压紧板，再次将板从最底端送往斜面上部，如此往复．已知板的质量为
．滚轮边缘线速度恒为
．滚轮对板的压力
，滚轮与板间的动摩擦因数为
，g取
。
求：（1）在滚轮作用下板上升的加速度：
（2）板加速至与滚轮速度相同时前进的距离
（3）每个周期中滚轮对金属板所做的功；
（4）板往复运动的周期．
如图是一个十字路口的示意图，每条停车线到十字路中心O的距离均为20m。一人骑电动助力车以7m/s的速度到达停车线（图中A点）时，发现左前方道路一辆轿车正以8m/s的速度驶来，车头已抵达停车线（图中B），设两车均沿道路中央作直线运动，助力车可视为质点，轿车长4.8m，宽度可不计。
（1）请通过计算判断两车保持上述速度匀速运动，是否会发生相撞事故？
（2）若轿车保持上述速度匀速运动，而助力车立即作匀加速直线运动，为避免发生相撞事故，助力车的加速度至少要多大？
一辆载重汽车以v0=20m/s的正常速度匀1速行驶，当通过500m长的大桥时，汽车必须以10m/s的速度运行，汽车到达大桥前先作匀减速运动，汽车离开大桥后作匀加速运动，最后达到正常速度行驶，减速过程和加速过程汽车的加速度大小均为0.5m/s2，
(1)为保证汽车过桥速度为10m/s，求汽车应该在离大桥多远处减速。
(2)从汽车减速开始计时，到汽车恢复正常速度，求汽车的运动时间。
(3)求汽车因为过桥而耽误的时间。
甲物体从阳台自由下落，已知物体在下落过程中最后2秒的位移是60m。(g=10m/s2)
（1）阳台离地面的高度
（2）最后1s的平均速度为多少
（3）若甲释放2s后，乙也从阳台释放，要甲、乙同时落地，需给乙多大的向下的初速度.
粤公网安备 44130202000953号