如图所示，真空中水平放置的两个相同极板Y和Y＇长为l，相距d，足够大的竖直屏与两板右侧边缘相距b。在两板间加上可调偏转电压U＇。一束质量为m、带电荷量为＋q的粒子（不计重力）从两板左侧中点A以初速度v0沿水平方向射入电场且能穿出。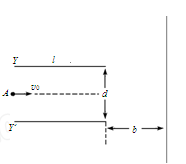
（1）证明粒子飞出电场后的速度方向的反向延长线交于两板间的中心O点；
（2）求两板间所加偏转电压U的范围；
（3）求粒子可能到达屏上区域的长度。
如图所示，质量为m=4kg的物体静止在水平面上，在外力F=25N作用下开始运动，已知F与水平方向夹角为37°，物体位移为5m时，具有50J的动能．求：（取g=10m/s2）
（1）此过程中，物体克服摩擦力所做的功；（sin37°=0.6，cos37°=0.8）
（2）物体与水平面间的动摩擦因数．
如图所示，抗震救灾运输机在某场地通过倾角为
的光滑斜面卸放物资，斜面与粗糙的水平面平滑连接。现将一包装盒（可视为质点）从斜面上A点由静止释放，最终停在水平面上的C点。已知A点距水平面的高度
，B点距C点的距离
。（包装盒经过B点时速度大小不变，
），求：
（1）包装盒在运动过程中的最大速度；
（2）包装盒与水平面间的动摩擦因数
；
（3）包装盒从A点释放后，经过时间
时速度的大小。
如图所示，光滑金属球的质量
，它的左侧紧靠竖直的墙壁，右侧置于倾角
的斜面体上。已知斜面体处于水平地面上保持静止状态，
，
，
，求：
（1）墙壁对金属球的弹力大小和金属球对斜面体的弹力大小；
（2）水平地面对斜面体的摩擦力的大小。
一辆在绵隧高速公路上以
的速度行驶的小汽车，突然发现同一车道的正前方
处停有一辆故障车，由于无法从其它车道避让，司机从发现前方故障车道开始制动有
的反应时间，制动后小汽车以
的加速度做匀减速直线运动，请你通过计算判定这辆小汽车是否会与前方故障车发生追尾事故？
的小球用细绳栓着吊在行驶的汽车后壁上，绳与竖直方向夹角为
。已知
，
，
，求；
向右匀减速行驶时，细线对小球的拉力和小球对车后壁的压力。
向右匀减速行驶时，细线对小球的拉力和小球对车后壁的压力。
粤公网安备 44130202000953号