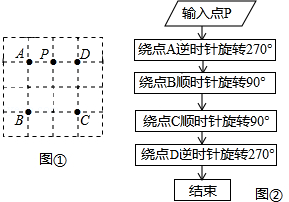
图①是电子屏幕的局部示意图，4×4网格的每个小正方形边长均为_优题课试题网

首页 / 初中数学 / 试题详细

更新 2022-09-03
科目数学
题型填空题
难度较难
浏览 963

山东省滨州市九年级上学期期中考试数学试卷

上一题下一题

图①是电子屏幕的局部示意图，4×4网格的每个小正方形边长均为1，每个小正方形顶点叫做格点，点A，B，C，D在格点上，光点P从AD的中点出发，按图②的程序移动
（1）请在图①中用圆规画出光点P经过的路径；
（2）在图①中，所画图形是图形（填“轴对称”或“中心对称”），所画图形的周长是（结果保留π）．

登录免费查看答案和解析

相关试题

因式分解： $a^{3} - a =$ 　　．

题型：未知
难度：未知

收藏答案/解析

正方形 $A_{1} B_{1} C_{1} O$ ， $A_{2} B_{2} C_{2} C_{1}$ ， $A_{3} B_{3} C_{3} C_{2}$ ， $\dots$ 按如图的方式放置，点 $A_{1}$ ， $A_{2}$ ， $A_{3} \dots$ 和点 $C_{1}$ ， $C_{2}$ ， $C_{3} \dots$ 分别在直线 $y = x + 1$ 和 $x$ 轴上，则点 $B_{n}$ 的坐标为　　． $(n$ 为正整数）

题型：未知
难度：未知

收藏答案/解析

如图，已知直线 $y = k_{1} x + b$ 与 $x$ 轴、 $y$ 轴相交于 $P$ 、 $Q$ 两点，与 $y = \frac{k_{2}}{x}$ 的图象相交于 $A (- 2, m)$ 、 $B (1, n)$ 两点，连接 $OA$ 、 $OB$ ，给出下列结论：① $k_{1} k_{2} < 0$ ；② $m + \frac{1}{2} n = 0$ ；③ $S_{ΔAOP} = S_{ΔBOQ}$ ；④不等式 $k_{1} x + b > \frac{k_{2}}{x}$ 的解集是 $x < - 2$ 或 $0 < x < 1$ ，其中正确的结论的序号是　　．

题型：未知
难度：未知

收藏答案/解析

如图， $C$ 为半圆内一点， $O$ 为圆心，直径 $AB$ 长为 $2 cm$ ， $∠ BOC = 60 °$ ， $∠ BCO = 90 °$ ，将 $ΔBOC$ 绕圆心 $O$ 逆时针旋转至△ $B' OC'$ ，点 $C'$ 在 $OA$ 上，则边 $BC$ 扫过区域（图中阴影部分）的面积为　　 $c m^{2}$ ．（结果保留 $π)$

题型：未知
难度：未知

收藏答案/解析

如图，点 $P_{1}$ ， $P_{2}$ ， $P_{3}$ ， $P_{4}$ 均在坐标轴上，且 $P_{1} P_{2} ⊥ P_{2} P_{3}$ ， $P_{2} P_{3} ⊥ P_{3} P_{4}$ ，若点 $P_{1}$ ， $P_{2}$ 的坐标分别为 $(0, - 1)$ ， $(- 2, 0)$ ，则点 $P_{4}$ 的坐标为　　．

题型：未知
难度：未知

收藏答案/解析

相关知识点

对称式和轮换对称式

推荐套卷

热门套卷

粤ICP备20024846号

粤公网安备

粤公网安备 44130202000953号

Copyright ©2020-2024 优题课 youtike.com 版权所有 Powered by：Youtike Platform 6.6.5

声明：本网站部分内容由互联网用户自发贡献自行上传，本网站不拥有所有权，也不承担相关法律责任。
如果您发现有涉嫌版权的内容，欢迎发送邮件至：service@youtike.com 或联系QQ：267757 进行举报，一经查实，本站将立刻删除涉嫌侵权内容。