(12分)在光滑水平面上固定一个内壁光滑的竖直圆环S(右图为俯视图),圆环半径为R="lm." 一根长r=0.5m的绝缘细线一端固定于圆环圆心D点,另一端系住一个质量为m=0.2kg、带电量为q=+5×10 - 5C的小球.空间有一场强为E=4xl04N/C的匀强电场,电场方向与水平面平行.将细线拉至与电场线平行,给小球大小为10m/s、方向垂直于电场线的初速度vo.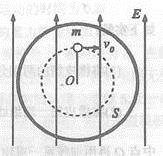
(1)求当小球转过90°时的速度大小;
(2)若当小球转过90°时,细线突然断裂,小球继续运动,碰到圆环后不反弹,碰撞后,小球垂直于碰撞切面方向的速度因能量损失减小为零,平行于碰撞切面方向的速度大小保持不变.之后小球沿圆环内壁继续做圆周运动.求这一运动过程中的速度的最小值.
(3)从初始位置开始,要使小球在运动过程中,细线始终保持不松弛,求电场强度E的大小所需满足的条件.
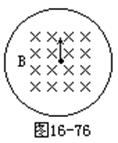
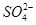 ,
,
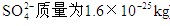 ,
,
 粤公网安备 44130202000953号
粤公网安备 44130202000953号