在工厂的流水线上安装水平传送带，可以把沿斜面滑下的工件用水平传送带进行传送，可大大提高工作效率。如图所示，一倾角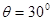
的光滑斜面下端与水平传送带相连，一工件从
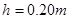高处的A点由静止滑下后到达B点的速度为
，接着以滑上水平放置的传送带。已知：传送带长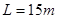
，向右保持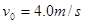
的运行速度不变，工件与传送带间的动摩擦因数
，
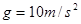，空气阻力不计，工件可看成质点。求：
（1）求工件从A点由静止下滑到离开传送带C点所用的时间。
（2）假设传送带是白色的，工件为一煤块，则工件从B滑到C的过程中，在传送带上留下黑色痕迹的长度S=？
相关试题
一汽车以20m/s的速度在公路上匀速行驶，发现前方有一障碍物后急刹车，刹车时加速度大小为5m/s2，
（１）求刹车５秒后的位移
（２）如果驾驶员的反应时间是0.5秒，则汽车以20m/s的速度在公路上匀速行驶时,驾驶员至少应距离障碍物多远发现障碍物，才不会发生事故？
粤公网安备 44130202000953号