如图所示,一平板车以某一速度v0匀速行驶,某时刻一货箱(可视为质点)无初速度地放置于平板车上,货箱离车后端的距离为l=3m,货箱放入车上的同时,平板车开始刹车,刹车过程可视为做a=4m/s2的匀减速直线运动.已知货箱与平板车之间的动摩擦因数为μ=0.2,g=10m/s2.为使货箱不从平板车上掉下来,平板车匀速行驶的速度v0应满足什么条件?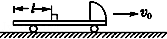
如图所示,一平板车以某一速度v0匀速行驶,某时刻一货箱(可视为质点)无初速度地放置于平板车上,货箱离车后端的距离为l=3m,货箱放入车上的同时,平板车开始刹车,刹车过程可视为做a=4m/s2的匀减速直线运动.已知货箱与平板车之间的动摩擦因数为μ=0.2,g=10m/s2.为使货箱不从平板车上掉下来,平板车匀速行驶的速度v0应满足什么条件?